Thermodynamics
In physics, thermodynamics (from the Greek θερμη, therme, meaning "heat"[1] and δυναμις, dynamis, meaning "power") is the study of the transformation of energy into different forms and its relation to macroscopic variables such as temperature, pressure, and volume. Its underpinnings, based upon statistical predictions of the collective motion of particles from their microscopic behavior, is the field of statistical thermodynamics, a branch of statistical mechanics.[2][3][4] Roughly, heat means "energy in transit" and dynamics relates to "movement"; thus, in essence thermodynamics studies the movement of energy and how energy instills movement. Historically, thermodynamics developed out of need to increase the efficiency of early steam engines.[5]
The starting point for most thermodynamic considerations are the laws of thermodynamics, which postulate that energy can be exchanged between physical systems as heat or work.[6] They also postulate the existence of a quantity named entropy, which can be defined for any system.[7] In thermodynamics, interactions between large ensembles of objects are studied and categorized. Central to this are the concepts of system and surroundings. A system is composed of particles, whose average motions define its properties, which in turn are related to one another through equations of state. Properties can be combined to express internal energy and thermodynamic potentials, which are useful for determining conditions for equilibrium and spontaneous processes.
With these tools, thermodynamics describes how systems respond to changes in their surroundings. This can be applied to a wide variety of topics in science and engineering, such as engines, phase transitions, chemical reactions, transport phenomena, and even black holes. The results of thermodynamics are essential for other fields of physics and for chemistry, chemical engineering, aerospace engineering, mechanical engineering, cell biology, biomedical engineering, materials science, and economics to name a few.[8][9]
The laws of thermodynamics
In thermodynamics, there are four laws of very general validity, and as such they do not depend on the details of the interactions or the systems being studied. Hence, they can be applied to systems about which one knows nothing other than the balance of energy and matter transfer. Examples of this include Einstein's prediction of spontaneous emission around the turn of the 20th century and current research into the thermodynamics of black holes.
The four laws are:
- Zeroth law of thermodynamics, stating that thermodynamic equilibrium is an equivalence relation.
-
- If two thermodynamic systems are separately in thermal equilibrium with a third, they are also in thermal equilibrium with each other.
-
- The change in the internal energy of a closed thermodynamic system is equal to the sum of the amount of heat energy supplied to the system and the work done on the system.
-
- The total entropy of any isolated thermodynamic system tends to increase over time, approaching a maximum value.
-
- As a system asymptotically approaches absolute zero of temperature all processes virtually cease and the entropy of the system asymptotically approaches a minimum value; also stated as: "the entropy of all systems and of all states of a system is zero at absolute zero" or equivalently "it is impossible to reach the absolute zero of temperature by any finite number of processes".
- Onsager reciprocal relations (sometimes called the Fourth Law of Thermodynamics)
-
- Express the equality of certain relations between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists.
-
- See also: Bose–Einstein condensate and negative temperature.
Zeroth law of thermodynamics
Laws of thermodynamics Zeroth Law First Law Second Law Third Law Fundamental Relation The zeroth law of thermodynamics is a generalized statement about thermal equilibrium between bodies in contact. It is the result of the definition and properties of temperature [1]. A common phrasing of the zeroth law of thermodynamics is:
If two thermodynamic systems are in thermal equilibrium with a third, they are also in thermal equilibrium with each other.
The law can be expressed in mathematical form as a simple transitive relation between the temperature T of the bodies A, B, and C:


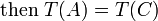
Contents |
History
The term zeroth law was coined by Ralph H. Fowler[citation needed]. In many ways, the law is more fundamental than any of the others[disambiguation needed]. However, the need to state it explicitly as a law was not perceived until the first third of the 20th century, long after the first three laws were already widely in use and named as such, hence the zero numbering.Thermal equilibrium
A system is said to be in thermal equilibrium when its temperature is stable (i.e does not change over time). Mathematically, this could be expressed as:
Thermal equilibrium between many systems
Many systems are said to be in equilibrium if the small exchanges (due to Brownian motion, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.
Consider N systems in adiabatic isolation from the rest of the universe (i.e no heat exchange is possible outside of these N systems), all of which have a constant volume and composition, who can only exchange heat with one another.
The combined first and second laws relate the fluctuations in total energy δU to the temperature of the ith system Ti and the entropy fluctuation in the ith system δSi by,
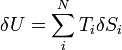 .
.
The adiabatic isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes,
 ,
,
that is, entropy can only be exchanged between the N systems. This constraint can be used to re-arrange the expression for the total energy fluctuation to give,
 ,
,
where Tj is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, so we arrive at,
 ,
,
which can be thought of as the vanishing of the product of an anti-symmetric matrix Ti − Tj and a vector of entropy fluctuations δSi. In order for a non-trivial solution to exist,
 ,
,
the determinant of the matrix formed by Ti − Tj must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN anti-symmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish, Ti − Tj = 0, in order to obtain a vanishing determinant, and hence Ti = Tj at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.
The zeroth law solves this odd vs. even paradox, because it can readily be used to reduce an odd-numbered system to an even number by considering any three of the N systems and eliminating one by application of its principle, and hence reduce the problem to even N which subsequently leads to the same equilibrium condition that we expect in every case, i.e., Ti = Tj. The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials), and therefore the zeroth law carries implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of anti-symmetry that exists in the first and second laws.
Temperature and the zeroth law
It is often claimed, for instance by Max Planck in his influential textbook on thermodynamics, that this law proves that we can define a temperature function, or more informally, that we can 'construct a thermometer'. Whether this is true is a subject in the philosophy of thermal and statistical physics.
In the space of thermodynamic parameters, zones of constant temperature will form a surface, which provides a natural order of nearby surfaces. It is then simple to construct a global temperature function that provides a continuous ordering of states. Note that the dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters (thus, for an ideal gas described with 3 thermodynamic parameter P, V and n, they are 2D surfaces). The temperature so defined may indeed not look like the Celsius temperature scale, but it is a temperature function.
For example, if two systems of ideal gas are in equilibrium, then P1V1/N1 = P2V2/N2 where Pi is the pressure in the ith system, Vi is the volume, and Ni is the 'amount' (in moles, or simply number of atoms) of gas.
The surface PV / N = const defines surfaces of equal temperature, and the obvious (but not only) way to label them is to define T so that PV / N = RT where R is some constant. These systems can now be used as a thermometer to calibrate other systems.
First law of thermodynamics
In thermodynamics, the first law of thermodynamics is an expression of the more universal physical law of the conservation of energy. Succinctly, the first law of thermodynamics states:
“ The increase in the internal energy of a system is equal to the amount of energy added by heating the system, minus the amount lost as a result of the work done by the system on its surroundings. ” Laws of thermodynamics Zeroth Law First Law Second Law Third Law Fundamental Relation Contents
Description
The first law of thermodynamics basically states that a thermodynamic system can store or hold energy and that this internal energy is conserved. Heat is a process by which energy is added to a system from a high-temperature source, or lost to a low-temperature sink. In addition, energy may be lost by the system when it does mechanical work on its surroundings, or conversely, it may gain energy as a result of work done on it by its surroundings. The first law states that this energy is conserved: The change in the internal energy is equal to the amount added by heating minus the amount lost by doing work on the environment. The first law can be stated mathematically as:
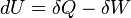
where dU is a small increase in the internal energy of the system, δQ is a small amount of heat added to the system, and δW is a small amount of work done by the system.
Notice that a lot of textbooks (e.g., Greiner Neise Stocker) formulate the first law as:
The only difference here is that δW is the work done on the system. So, when the system (eg. gas) expands the work done on the system is − PdV whereas in the previous formulation of the first law, the work done by the gas while expanding is PdV. In any case, both give the same result when written explicitly as:
The δ's before the heat and work terms are used to indicate that they describe an increment of energy which is to be interpreted somewhat differently than the dU increment of internal energy. Work and heat are processes which add or subtract energy, while the internal energy U is a particular form of energy associated with the system. Thus the term "heat energy" for δQ means "that amount of energy added as the result of heating" rather than referring to a particular form of energy. Likewise, the term "work energy" for δw means "that amount of energy lost as the result of work". Internal energy is the property of the system whereas work done or heat supplied is not The most significant result of this distinction is the fact that one can clearly state the amount of internal energy possessed by a thermodynamic system, but one cannot tell how much energy has flowed into or out of the system as a result of its being heated or cooled, nor as the result of work being performed on or by the system. The first explicit statement of the first law of thermodynamics was given by Rudolf Clausius in 1850: "There is a state function E, called ‘energy’, whose differential equals the work exchanged with the surroundings during an adiabatic process."
Mathematical formulation
The mathematical statement of the first law is given by:
where dU is the infinitesimal increase in the internal energy of the system, δQ is the infinitesimal amount of heat added to the system, and δw is the infinitesimal amount of work done by the system. The infinitesimal heat and work are denoted by δ rather than d because, in mathematical terms, they are not exact differentials. In other words, they do not describe the state of any system. The integral of an inexact differential depends upon the particular "path" taken through the space of thermodynamic parameters while the integral of an exact differential depends only upon the initial and final states. If the initial and final states are the same, then the integral of an inexact differential may or may not be zero, but the integral of an exact differential will always be zero. The path taken by a thermodynamic system through state space is known as a thermodynamic process.
An expression of the first law can be written in terms of exact differentials by realizing that the work that a system does is, in case of a reversible process, equal to its pressure times the infinitesimal change in its volume. In other words δw = PdV where P is pressure and V is volume. Also, for a reversible process, the total amount of heat added to a system can be expressed as δQ = TdS where T is temperature and S is entropy. Therefore, for a reversible process, :
Since U, S and V are thermodynamic functions of state, the above relation holds also for non-reversible changes. The above equation is known as the fundamental thermodynamic relation.
In the case where the number of particles in the system is not necessarily constant and may be of different types, the first law is written:
where dNi is the (small) number of type-i particles added to the system, and μi is the amount of energy added to the system when one type-i particle is added, where the energy of that particle is such that the volume and entropy of the system remains unchanged. μi is known as the chemical potential of the type-i particles in the system. The statement of the first law, using exact differentials is now:
If the system has more external variables than just the volume that can change, the fundamental thermodynamic relation generalizes to:
Here the Xi are the generalized forces corresponding to the external variables xi.
A useful idea from mechanics is that the energy gained by a particle is equal to the force applied to the particle multiplied by the displacement of the particle while that force is applied. Now consider the first law without the heating term: dU = − PdV. The pressure P can be viewed as a force (and in fact has units of force per unit area) while dV is the displacement (with units of distance times area). We may say, with respect to this work term, that a pressure difference forces a transfer of volume, and that the product of the two (work) is the amount of energy transferred as a result of the process.
It is useful to view the TdS term in the same light: With respect to this heat term, a temperature difference forces a transfer of entropy, and the product of the two (heat) is the amount of energy transferred as a result of the process. Here, the temperature is known as a "generalized" force (rather than an actual mechanical force) and the entropy is a generalized displacement.
Similarly, a difference in chemical potential between groups of particles in the system forces a trasfer of particles, and the corresponding product is the amount of energy transferred as a result of the process. For example, consider a system consisting of two phases: liquid water and water vapor. There is a generalized "force" of evaporation which drives water molecules out of the liquid. There is a generalized "force" of condensation which drives vapor molecules out of the vapor. Only when these two "forces" (or chemical potentials) are equal will there be equilibrium, and the net transfer will be zero.
The two thermodynamic parameters which form a generalized force-displacement pair are termed "conjugate variables". The two most familiar pairs are, of course, pressure-volume, and temperature-entropy.
Application of the first law
Isobaric process
An isobaric process is a thermodynamic process in which the pressure stays constant: Δp = 0 The term derives from the Greek isos, "equal," and barus, "heavy." The heat transferred to the system does work but also changes the internal energy of the system:
According to the first law of thermodynamics, where W is nn work done by the system, U is internal energy, and Q is heat. Pressure-volume work (by the system) is defined as: (Δ means change over the whole process, it doesn't mean differential)
but since pressure is constant, this means that
 .
.
Applying the ideal gas law, this becomes
assuming that the quantity of gas stays constant (e.g. no phase change during a chemical reaction). Since it is generally true that[citation needed]
then substituting the last two equations into the first equation produces:
-
 .
.
The quantity in parentheses is equivalent to the molar specific heat for constant pressure:
- cp = cV + R
and if the gas involved in the isobaric process is monatomic then  and
and  .
.
An isobaric process is shown on a P-V diagram as a straight horizontal line, connecting the initial and final thermostatic states. If the process moves towards the right, then it is an expansion. If the process moves towards the left, then it is a compression.
Defining Enthalpy
An isochoric process is described by the equation Q = ΔU. It would be convenient to have a similar equation for isobaric processes. Substituting the second equation into the first yields
The quantity U + p V is a state function so that it can be given a name. It is called enthalpy, and is denoted as H. Therefore an isobaric process can be more succinctly described as
 .
.
Variable density viewpoint
A given quantity (mass M) of gas in a changing volume produces a change in density ρ. In this context the ideal gas law is written
- R(T ρ) = M P
where T is thermodynamic temperature above absolute zero. When R and M are taken as constant, then pressure P can stay constant as the density-tempertature quadrant (ρ,T ) undergoes a squeeze mapping. It is this context that explains Peter Olver's use of the term isobaric group when referring to the group of squeeze mappings on page 217 of his book Classical Invariant Theory (1999).
Isochoric process
 Isochoric Process in the Pressure volume diagram. In this diagram, pressure increases, but volume remains constant.
Isochoric Process in the Pressure volume diagram. In this diagram, pressure increases, but volume remains constant.An isochoric process, also called an isovolumetric process, is a process during which volume remains constant. The name is derived from the Greek isos, "equal", and khora, "place."
If an ideal gas is used in an isochoric process, and the quantity of gas stays constant, then the increase in energy is proportional to an increase in temperature and pressure. Take for example a gas heated in a rigid container: the pressure and temperature of the gas will increase, but the volume will remain the same.
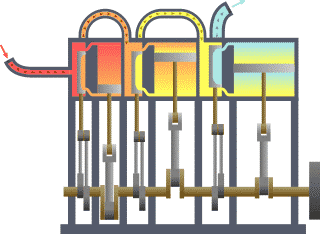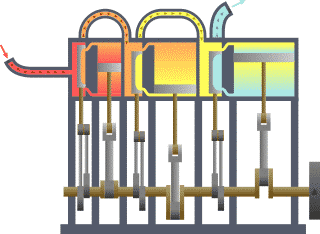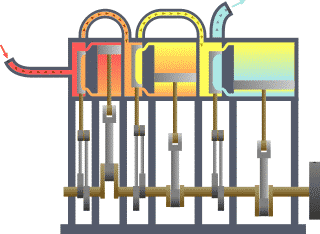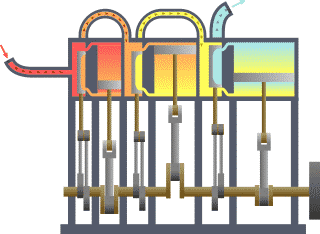
In the ideal Otto cycle we found an example of an isochoric process when we assume an instantaneous burning of the gasoline-air mixture in an internal combustion engine car. There is an increase in the temperature and the pressure of the gas inside the cylinder while the volume remains the same.
Equations
If the volume stays constant (ΔV = 0), this implies that the process does no pressure-volume work, since such work is defined by
- ΔW = PΔV,
where P is pressure (no minus sign; this is work done by the system).
By applying the first law of thermodynamics, we can deduce that ΔU the change in the system's internal energy, is
- ΔU = Q
for an isochoric process: all the heat being transferred to the system is added to the system's internal energy, U. If the quantity of gas stays constant, then this increase in energy is proportional to an increase in temperature,
- Q = mCVΔT
where CV is molar specific heat for constant volume.
On a pressure volume diagram, an isochoric process appears as a straight vertical line. Its thermodynamic conjugate, an isobaric process would appear as a straight horizontal line.
Isothermal process
An isothermal process is a change in which the temperature of the system stays constant: ΔT = 0. This typically occurs when a system is in contact with an outside thermal reservoir (heat bath), and the change occurs slowly enough to allow the system to continually adjust to the temperature of the reservoir through heat exchange. An alternative special case in which a system exchanges no heat with its surroundings (Q = 0) is called an adiabatic process. In other words, in an isothermal process, ΔT = 0 but Q
 0, while in an adiabatic process, ΔT
0, while in an adiabatic process, ΔT 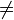 0 but Q = 0.
0 but Q = 0.Contents
Details for an ideal gas
 Several isotherms of an ideal gas on a p-V diagram
Several isotherms of an ideal gas on a p-V diagramFor the special case of a gas to which Boyle's law applies, the product pV is a constant if the gas is kept at isothermal conditions. The value of the constant is nRT, where n is the number of moles of gas present and R is the ideal gas constant. In other words, the ideal gas law pV = nRT applies. This means that

holds. The family of curves generated by this equation is shown in the graph presented here. Each curve is called an isotherm. Such graphs are termed indicator diagrams and were first used by James Watt and others to monitor the efficiency of engines. The temperature corresponding to each curve in the figure increases from the lower left to the upper right.
Calculation of work
In thermodynamics, the work involved when a gas changes from state A to state B is simply
For an isothermal, reversible process, this integral equals the area under the relevant pressure-volume isotherm, and is indicated in yellow in the figure at right for an ideal gas. Again p = nRT / V applies and so
It is also worth noting that since the temperature is held constant during this change then the internal energy of the system is constant, and so ΔU = 0. From ΔU = Q - W it follows that Q = W for this same isothermal process. In other words,
Applications
Isothermal processes can occur in any kind of system, including highly structured machines, and even living cells. Various parts of the cycles of some heat engines are carried out isothermally and may be approximated by a Carnot cycle.
Isentropic process
In thermodynamics, an isentropic process (iso = "equal" (Greek); entropy = "disorder") is one during which the entropy of the system remains constant. [1][2] It can be proved that any reversible adiabatic process is an isentropic process.
Contents
Background
Second law of thermodynamics states that,

where δQ is the amount of energy the system gains by heating, T is the temperature of the system, and dS is the change in entropy. The equal sign will hold for a reversible process. For a reversible isentropic process, there is no transfer of heat energy and therefore the process is also adiabatic. For an irreversible process, the entropy will increase. Hence removal of heat from the system (cooling) is necessary to maintain a constant internal entropy for an irreversible process so as to make it isentropic. Thus an irreversible isentropic process is not adiabatic.
For reversible processes, an isentropic transformation is carried out by thermally "insulating" the system from its surroundings. Temperature is the thermodynamic conjugate variable to entropy, and so the conjugate process would be an isothermal process in which the system is thermally "connected" to a constant-temperature heat bath.
Isentropic flow
An isentropic flow is a flow that is both adiabatic and reversible. That is, no energy is added to the flow, and no energy losses occur due to friction or dissipative effects. For an isentropic flow of a perfect gas, several relations can be derived to define the pressure, density and temperature along a streamline.
Derivation of the isentropic relations
For a closed system, the total change in energy of a system is the sum of the work done and the heat added,
- dU = dW + dQ
The work done on a system by changing the volume is,
- dW = − pdV
where p is the pressure and V the volume. The change in enthalpy (H = U + pV) is given by,
- dH = dU + pdV + Vdp = nCpdT
Since a reversible process is adiabatic (i.e. no heat transfer occurs), so dQ = 0,dS = 0. This leads to two important observations,
- dU = − pdV, and
- dH = Vdp or dQ = dH − Vdp = 0
- dQ = TdS => dS = (1 / T)dH − (V / T)dp
The heat capacity ratio can be written as,
For a perfect gas γ is constant. Hence on integrating the above equation, assuming a perfect gas, we get
 i.e.
i.e.
Using the equation of state for an ideal gas, pV = nRT,
- also, for constant C_p = C_v + R (per mole),
 and
and 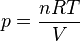


Thus for insentropic processes with an ideal gas,
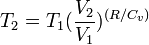 or
or 
Table of isentropic relations for an ideal gas
Derived from:
-
- Where:
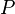 = Pressure
= Pressure = Volume
= Volume = Ratio of specific heats
= Ratio of specific heats = Temperature
= Temperature = Mass
= Mass = Gas constant for the specific gas
= Gas constant for the specific gas = Density
= Density
- Where:
Adiabatic process
In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which no heat is transferred to or from the working fluid. The term "adiabatic" literally means impassable (from Greek ἀ-διὰ-βαῖνειν, not-through-to pass), corresponding here to an absence of heat transfer. Conversely, a process that involves heat transfer (addition or loss of heat to the surroundings) is generally called diabatic.
For example, an adiabatic boundary is a boundary that is impermeable to heat transfer and the system is said to be adiabatically (or thermally) insulated; an insulated wall approximates an adiabatic boundary. Another example is the adiabatic flame temperature, which is the temperature that would be achieved by a flame in the absence of heat loss to the surroundings. An adiabatic process that is reversible is also called an isentropic process. Additionally, an adiabatic process that is irreversible and extracts no work is in an isenthalpic process, such as viscous drag, progressing towards a nonnegative change in entropy.
One opposite extreme—allowing heat transfer with the surroundings, causing the temperature to remain constant—is known as an isothermal process. Since temperature is thermodynamically conjugate to entropy, the isothermal process is conjugate to the adiabatic process for reversible transformations.
A transformation of a thermodynamic system can be considered adiabatic when it is quick enough that no significant heat is transferred between the system and the outside. At the opposite extreme, a transformation of a thermodynamic system can be considered isothermal if it is slow enough so that the system's temperature remains constant by heat exchange with the outside.
Contents |
Adiabatic heating and cooling
Adiabatic changes in temperature occur due to changes in pressure of a gas while not adding or subtracting any heat.
Adiabatic heating occurs when the pressure of a gas is increased from work done on it by its surroundings, ie a piston. Diesel engines rely on adiabatic heating during their compression stroke to elevate the temperature sufficiently to ignite the fuel. Similarly jet engines rely upon adiabatic heating to create the correct compression of the air to enable fuel to be injected and ignition to then occur.
Adiabatic heating also occurs in the Earth's atmosphere when an air mass descends, for example, in a katabatic wind or Foehn wind flowing downhill.
Adiabatic cooling occurs when the pressure of a substance is decreased as it does work on its surroundings. Adiabatic cooling does not have to involve a fluid. One technique used to reach very low temperatures (thousandths and even millionths of a degree above absolute zero) is adiabatic demagnetisation, where the change in magnetic field on a magnetic material is used to provide adiabatic cooling. Adiabatic cooling also occurs in the Earth's atmosphere with orographic lifting and lee waves, and this can form pileus or lenticular clouds if the air is cooled below the dew point.
Rising magma also undergoes adiabatic cooling before eruption.
Such temperature changes can be quantified using the ideal gas law, or the hydrostatic equation for atmospheric processes.
It should be noted that no process is truly adiabatic. Many processes are close to adiabatic and can be easily approximated by using an adiabatic assumption, but there is always some heat loss. There is no such thing as a perfect insulator.
Ideal gas (reversible case only)
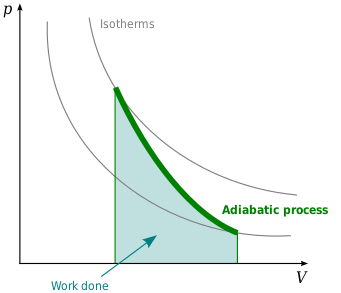
The mathematical equation for an ideal fluid undergoing a reversible (i.e., no entropy generation) adiabatic process is
where P is pressure, V is volume, and
CP being the specific heat for constant pressure and CV being the specific heat for constant volume. α comes from the number of degrees of freedom divided by 2 (3/2 for monatomic gas, 5/2 for diatomic gas). For a monatomic ideal gas, γ = 5 / 3, and for a diatomic gas (such as nitrogen and oxygen, the main components of air) γ = 7 / 5. Note that the above formula is only applicable to classical ideal gases and not Bose-Einstein or Fermi gases.
For reversible adiabatic processes, it is also true that
where T is an absolute temperature.
This can also be written as
Derivation of continuous formula
The definition of an adiabatic process is that heat transfer to the system is zero, δQ = 0. Then, according to the first law of thermodynamics,
where dU is the change in the internal energy of the system and δW is work done by the system. Any work (δW) done must be done at the expense of internal energy U, since no heat δQ is being supplied from the surroundings. Pressure-volume work δW done by the system is defined as
However, P does not remain constant during an adiabatic process but instead changes along with V.
It is desired to know how the values of dP and dV relate to each other as the adiabatic process proceeds. For an ideal gas the internal energy is given by
where R is the universal gas constant and n is the number of moles in the system (a constant).
Differentiating Equation (3) and use of the ideal gas law, PV = nRT, yields
Equation (4) is often expressed as  because CV = αR.
because CV = αR.
Now substitute equations (2) and (4) into equation (1) to obtain
simplify:
and divide both sides by PV:
After integrating the left and right sides from V0 to V and from P0 to P and changing the sides respectively,
Exponentiate both sides,
and eliminate the negative sign to obtain
Therefore,
and
Derivation of discrete formula
The change in internal energy of a system, measured from state 1 to state 2, is equal to
At the same time, the work done by the pressure-volume changes as a result from this process, is equal to
Since we require the process to be adiabatic, the following equation needs to be true
Substituting (1) and (2) in (3) leads to
or
If it's further assumed that there are no changes in molar quantity (as often in practical cases), the formula is simplified to this one:
Graphing adiabats
An adiabat is a curve of constant entropy on the P-V diagram. Properties of adiabats on a P-V diagram are:
- Every adiabat asymptotically approaches both the V axis and the P axis (just like isotherms).
- Each adiabat intersects each isotherm exactly once.
- An adiabat looks similar to an isotherm, except that during an expansion, an adiabat loses more pressure than an isotherm, so it has a steeper inclination (more vertical).
- If isotherms are concave towards the "north-east" direction (45 °), then adiabats are concave towards the "east north-east" (31 °).
- If adiabats and isotherms are graphed severally at regular changes of entropy and temperature, respectively (like altitude on a contour map), then as the eye moves towards the axes (towards the south-west), it sees the density of isotherms stay constant, but it sees the density of adiabats grow. The exception is very near absolute zero, where the density of adiabats drops sharply and they become rare (see Nernst's theorem).
The following diagram is a P-V diagram with a superposition of adiabats and isotherms:
The isotherms are the red curves and the adiabats are the black curves. The adiabats are isentropic. Volume is the horizontal axis and pressure is the vertical axis.
Second law of thermodynamics
Laws of thermodynamics Zeroth Law First Law Second Law Third Law Fundamental Relation The second law of thermodynamics is an expression of the universal law of increasing entropy, stating that the entropy of an isolated system which is not in equilibrium will tend to increase over time, approaching a maximum value at equilibrium.
The second law traces its origin to French physicist Sadi Carnot's 1824 paper Reflections on the Motive Power of Fire, which presented the view that motive power (work) is due to the fall of caloric (heat) from a hot to cold body (working substance). In simple terms, the second law is an expression of the fact that over time, ignoring the effects of self-gravity, differences in temperature, pressure, and density tend to even out in a physical system that is isolated from the outside world. Entropy is a measure of how far along this evening-out process has progressed.
There are many versions of the second law, but they all have the same effect, which is to explain the phenomenon of irreversibility in nature.
Contents
Introduction
Versions of The Law
There are many ways of stating the second law of thermodynamics, but all are equivalent in the sense that each form of the second law logically implies every other form.[1] Thus, the theorems of thermodynamics can be proved using any form of the second law and third law
The formulation of the second law that refers to entropy directly is as follows:
In a system, a process that occurs will tend to increase the total entropy of the universe.
Thus, while a system can undergo some physical process that decreases its own entropy, the entropy of the universe (which includes the system and its surroundings) must increase overall. (An exception to this rule is a reversible or "isentropic" process, such as frictionless adiabatic compression.) Processes that decrease total entropy of the universe are impossible. If a system is at equilibrium, by definition no spontaneous processes occur, and therefore the system is at maximum entropy.
Also, due to Rudolf Clausius, is the simplest formulation of the second law, the heat formulation or Clausius statement:
Heat generally cannot spontaneously flow from a material at lower temperature to a material at higher temperature.
Informally, "Heat doesn't flow from cold to hot (without work input)", which is obviously true from everyday experience. For example in a refrigerator, heat flows from cold to hot, but only when aided by an external agent (i.e. the compressor). Note that from the mathematical definition of entropy, a process in which heat flows from cold to hot has decreasing entropy. This can happen in a non-isolated system if entropy is created elsewhere, such that the total entropy is constant or increasing, as required by the second law. For example, the electrical energy going into a refrigerator is converted to heat and goes out the back, representing a net increase in entropy.
The exception to this is in statistically unlikely events where hot particles will "steal" the energy of cold particles enough that the cold side gets colder and the hot side gets hotter, for an instant. Such events have been observed at a small enough scale where the likelihood of such a thing happening is large enough [2]. The mathematics involved in such an event are described by fluctuation theorem.
A third formulation of the second law, by Lord Kelvin, is the heat engine formulation, or Kelvin statement:
It is impossible to convert heat completely into work.
That is, it is impossible to extract energy by heat from a high-temperature energy source and then convert all of the energy into work. At least some of the energy must be passed on to heat a low-temperature energy sink. Thus, a heat engine with 100% efficiency is thermodynamically impossible.
Microscopic systems
Thermodynamics is a theory of macroscopic systems and therefore the second law applies only to macroscopic systems with well-defined temperatures. The smaller the scale, the less the second law applies. On scales of a few atoms, the second law has little application. For example, in a system of two molecules, there is a non-trivial probability that the slower-moving ("cold") molecule transfers energy to the faster-moving ("hot") molecule. Such tiny systems are outside the domain of classical thermodynamics, but they can be investigated in quantum thermodynamics by using statistical mechanics. For any isolated system with a mass of more than a few picograms, probabilities of observing a decrease in entropy approach zero.[3]
Energy dispersal
The second law of thermodynamics is an axiom of thermodynamics concerning heat, entropy, and the direction in which thermodynamic processes can occur. For example, the second law implies that heat does not spontaneously flow from a cold material to a hot material, but it allows heat to flow from a hot material to a cold material. Roughly speaking, the second law says that in an isolated system, concentrated energy disperses over time, and consequently less concentrated energy is available to do useful work. Energy dispersal also means that differences in temperature, pressure, and density even out. Again roughly speaking, thermodynamic entropy is a measure of energy dispersal, and so the second law is closely connected with the concept of entropy.
Overview
In a general sense, the second law says that temperature differences between systems in contact with each other tend to even out and that work can be obtained from these non-equilibrium differences, but that loss of heat occurs, in the form of entropy, when work is done.[4] Pressure differences, density differences, and particularly temperature differences, all tend to equalize if given the opportunity. This means that an isolated system will eventually come to have a uniform temperature. A heat engine is a mechanical device that provides useful work from the difference in temperature of two bodies:
During the 19th century, the second law was synthesized, essentially, by studying the dynamics of the Carnot heat engine in coordination with James Joule's Mechanical equivalent of heat experiments. Since any thermodynamic engine requires such a temperature difference, it follows that no useful work can be derived from an isolated system in equilibrium; there must always be an external energy source and a cold sink. By definition, perpetual motion machines of the second kind would have to violate the second law to function.
History
- See also: History of entropy
The first theory on the conversion of heat into mechanical work is due to Nicolas Léonard Sadi Carnot in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its environment.
Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law in 1850, in this form: heat does not spontaneously flow from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a liquid. From there he was able to infer the law of Sadi Carnot and the definition of entropy (1865).
Established in the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.
The Ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.
Using quantum mechanics it has been shown that the local von Neumann entropy is at its maximum value with an extremely high probability, thus proving the second law.[5] The result is valid for a large class of isolated quantum systems (e.g. a gas in a container). While the full system is pure and has therefore no entropy, the entanglement between gas and container gives rise to an increase of the local entropy of the gas. This result is one of the most important achievements of quantum thermodynamics.
Informal descriptions
The second law can be stated in various succinct ways, including:
- It is impossible to produce work in the surroundings using a cyclic process connected to a single heat reservoir (Kelvin, 1851).
- It is impossible to carry out a cyclic process using an engine connected to two heat reservoirs that will have as its only effect the transfer of a quantity of heat from the low-temperature reservoir to the high-temperature reservoir (Clausius, 1854).
- If thermodynamic work is to be done at a finite rate, free energy must be expended.[6]
Mathematical descriptions
In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:[7]
where N is the "equivalence-value" of all uncompensated transformations involved in a cyclical process. Later, in 1865, Clausius would come to define "equivalence-value" as entropy. On the heels of this definition, that same year, the most famous version of the second law was read in a presentation at the Philosophical Society of Zurich on April 24th, in which, in the end of his presentation, Clausius concludes:
The entropy of the universe tends to a maximum.
This statement is the best-known phrasing of the second law. Moreover, owing to the general broadness of the terminology used here, e.g. universe, as well as lack of specific conditions, e.g. open, closed, or isolated, to which this statement applies, many people take this simple statement to mean that the second law of thermodynamics applies virtually to every subject imaginable. This, of course, is not true; this statement is only a simplified version of a more complex description.
In terms of time variation, the mathematical statement of the second law for a closed system undergoing an arbitrary transformation is:
where
- S is the entropy and
- t is time.
It should be noted that statistical mechanics gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a microstate of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/√N where N is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically nil. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.
Available useful work
- See also: Available useful work (thermodynamics)
An important and revealing idealized special case is to consider applying the Second Law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an unlimited heat reservoir at temperature TR and pressure PR — so that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain TR; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain PR.
Whatever changes dS and dSR occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy Stot of the isolated total system must not decrease:
According to the First Law of Thermodynamics, the change dU in the internal energy of the sub-system is the sum of the heat δq added to the sub-system, less any work δw done by the sub-system, plus any net chemical energy entering the sub-system d ∑μiRNi, so that:
where μiR are the chemical potentials of chemical species in the external surroundings.
Now the heat leaving the reservoir and entering the sub-system is
where we have first used the definition of entropy in classical thermodynamics (alternatively, the definition of temperature in statistical thermodynamics); and then the Second Law inequality from above.
It therefore follows that any net work δw done by the sub-system must obey
It is useful to separate the work δw done by the subsystem into the useful work δwu that can be done by the sub-system, over and beyond the work pR dV done merely by the sub-system expanding against the surrounding external pressure, giving the following relation for the useful work that can be done:
It is convenient to define the right-hand-side as the exact derivative of a thermodynamic potential, called the availability or exergy X of the subsystem,
The Second Law therefore implies that for any process which can be considered as divided simply into a subsystem, and an unlimited temperature and pressure reservoir with which it is in contact,
i.e. the change in the subsystem's exergy plus the useful work done by the subsystem (or, the change in the subsystem's exergy less any work, additional to that done by the pressure reservoir, done on the system) must be less than or equal to zero.
Special cases: Gibbs and Helmholtz free energies
When no useful work is being extracted from the sub-system, it follows that
with the exergy X reaching a minimum at equilibrium, when dX=0.
If no chemical species can enter or leave the sub-system, then the term ∑ μiR Ni can be ignored. If furthermore the temperature of the sub-system is such that T is always equal to TR, then this gives:
If the volume V is constrained to be constant, then
where A is the thermodynamic potential called Helmholtz free energy, A=U−TS. Under constant volume conditions therefore, dA ≤ 0 if a process is to go forward; and dA=0 is the condition for equilibrium.
Alternatively, if the sub-system pressure p is constrained to be equal to the external reservoir pressure pR, then
where G is the Gibbs free energy, G=U−TS+PV. Therefore under constant pressure conditions, if dG ≤ 0, then the process can occur spontaneously, because the change in system energy exceeds the energy lost to entropy. dG=0 is the condition for equilibrium. This is also commonly written in terms of enthalpy, where H=U+PV.
Application
In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in X for an irreversible process and no change for a reversible process.
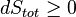 is equivalent to
is equivalent to 
This expression together with the associated reference state permits a design engineer working at the macroscopic scale (above the thermodynamic limit) to utilize the Second Law without directly measuring or considering entropy change in a total isolated system. (Also, see process engineer). Those changes have already been considered by the assumption that the system under consideration can reach equilibrium with the reference state without altering the reference state. An efficiency for a process or collection of processes that compares it to the reversible ideal may also be found (See second law efficiency.)
This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.
Criticisms
Owing to the somewhat ambiguous nature of the formulation of the second law, i.e. the postulate that the quantity heat divided by temperature increases in spontaneous natural processes, it has occasionally been subject to criticism as well as attempts to dispute or disprove it. Clausius himself even noted the abstract nature of the second law. In his 1862 memoir, for example, after mathematically stating the second law by saying that integral of the differential of a quantity of heat divided by temperature must be greater than or equal to zero for every cyclical process which is in any way possible:[7]
 ,
,
Clausius then stated:
Although the necessity of this theorem admits of strict mathematical proof if we start from the fundamental proposition above quoted it thereby nevertheless retains an abstract form, in which it is with difficulty embraced by the mind, and we feel compelled to seek for the precise physical cause, of which this theorem is a consequence.
Recall that heat and temperature are statistical, macroscopic quantities that become somewhat ambiguous when dealing with a small number of atoms.
Perpetual motion of the second kind
Before 1850, heat was regarded as an indestructible particle of matter. This was called the “material hypothesis”, as based principally on the views of Isaac Newton. It was on these views, partially, that in 1824 Sadi Carnot formulated the initial version of the second law. It soon was realized, however, that if the heat particle was conserved, and as such not changed in the cycle of an engine, that it would be possible to send the heat particle cyclically through the working fluid of the engine and use it to push the piston and then return the particle, unchanged, to its original state. In this manner perpetual motion could be created and used as an unlimited energy source. Thus, historically, people have always been attempting to create a perpetual motion machine so to disprove the second law.
Maxwell's Demon
In 1871, James Clerk Maxwell proposed a thought experiment, now called Maxwell's demon, which challenged the second law. This experiment reveals the importance of observability in discussing the second law. In other words, it requires a certain amount of energy to collect the information necessary for the demon to "know" the whereabouts of all the particles in the system. This energy requirement thus negates the challenge to the second law. This apparent paradox can also be reconciled from another perspective, by resorting to a use of information entropy.
Time's Arrow
The second law is a law about macroscopic irreversibility, and so may appear to violate the principle of T-symmetry. Boltzmann first investigated the link with microscopic reversibility. In his H-theorem he gave an explanation, by means of statistical mechanics, for dilute gases in the zero density limit where the ideal gas equation of state holds. He derived the second law of thermodynamics not from mechanics alone, but also from the probability arguments. His idea was to write an equation of motion for the probability that a single particle has a particular position and momentum at a particular time. One of the terms in this equation accounts for how the single particle distribution changes through collisions of pairs of particles. This rate depends of the probability of pairs of particles. Boltzmann introduced the assumption of molecular chaos to reduce this pair probability to a product of single particle probabilities. From the resulting Boltzmann equation he derived his famous H-theorem, which implies that on average the entropy of an ideal gas can only increase.
The assumption of molecular chaos in fact violates time reversal symmetry. It assumes that particle momenta are uncorrelated before collisions. If you replace this assumption with "anti-molecular chaos," namely that particle momenta are uncorrelated after collision, then you can derive an anti-Boltzmann equation and an anti-H-Theorem which implies entropy decreases on average. Thus we see that in reality Boltzmann did not succeed in solving Loschmidt's paradox. The molecular chaos assumption is the key element that introduces the arrow of time.
Applications to living systems
The second law of thermodynamics has been proven mathematically for thermodynamic systems, where entropy is defined in terms of heat divided by the absolute temperature. The second law is often applied to other situations, such as the complexity of life, or orderliness. [8] However it is incorrect to apply the second law of thermodynamics to any system that can subjectively be deemed "complex". In sciences such as biology and biochemistry the application of thermodynamics is well-established, e.g. biological thermodynamics. The general viewpoint on this subject is summarized well by biological thermodynamicist Donald Haynie; as he states: "Any theory claiming to describe how organisms originate and continue to exist by natural causes must be compatible with the first and second laws of thermodynamics." [9] This is very different, however, from the claim made by many creationists that evolution violates the second law of thermodynamics. In fact, evidence indicates that biological systems and obviously the evolution of those systems conform to the second law, since although biological systems may become more ordered, the net increase in entropy for the entire universe is still positive as a result of evolution. [10]
Complex systems
It is occasionally claimed that the second law is incompatible with autonomous self-organisation, or even the coming into existence of complex systems. This is a common creationist argument against evolution.[11] The entry self-organisation explains how this claim is a misconception. In fact, as hot systems cool down in accordance with the second law, it is not unusual for them to undergo spontaneous symmetry breaking, i.e. for structure to spontaneously appear as the temperature drops below a critical threshold. Complex structures, such as Bénard cells, also spontaneously appear where there is a steady flow of energy from a high temperature input source to a low temperature external sink.
Furthermore, a system that energy flows into and out of may decrease its local entropy provided the increase of the entropy to its surrounding that this process causes is greater than or equal to the local decrease in entropy. A good example of this is crystallization as a liquid cools, crystals begin to form inside it. While these crystals are more ordered than the liquid they originated from, in order for them to form they must release a great deal of heat, known as the latent heat of fusion. This heat flows out of the system and increases the entropy of its surroundings to a greater extent than the decrease of energy that the liquid undergoes in the formation of crystals.
An interesting situation to consider is that of a supercooled liquid perfectly isolated thermodynamically, into which a grain of dust is dropped. Here even though the system cannot export energy to its surroundings, it will still crystallize. Now however the release of latent heat will contribute to raising its own temperature. If this release of heat causes the temperature to reach the melting point before it has fully crystallized, then it shall remain a mixture of liquid and solid; if not, then it will be a solid at a significantly higher temperature than it previously was as a liquid. In both cases entropy from its disordered structure is converted into entropy of disordered motion.[citation needed]

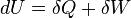
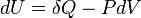
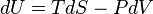














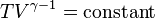








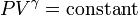



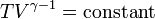

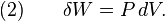

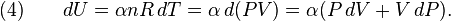





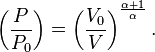




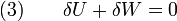




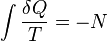
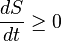











No comments:
Post a Comment