STATES OF MATTER
There are five main states of matter. Solids, liquids, gases, plasmas, and Bose-Einstein condensates are all different states of matter. Each of these states is also known as a phase. Elements and compounds can move from one phase to another phase when special physical forces are present. One example of those forces is temperature. The phase or state of matter can change when the temperature changes. Generally, as the temperature rises, matter moves to a more active state.
Phase describes a physical state of matter. The key word to notice is physical. Things only move from one phase to another by physical means. If energy is added (like increasing the temperature or increasing pressure) or if energy is taken away (like freezing something or decreasing pressure) you have created a physical change.
One compound or element can move from phase to phase, but still be the same substance. You can see water vapor over a boiling pot of water. That vapor (or gas) can condense and become a drop of water. If you put that drop in the freezer, it would become a solid. No matter what phase it was in, it was always water. It always had the same chemical properties. On the other hand, a chemical change would change the way the water acted, eventually making it not water, but something completely new.
SOLID BASICS
So what is a solid? Solids are usually hard because their molecules have been packed together. The closer your molecules are, the harder you are. Solids also can hold their own shape. A rock will always look like a rock unless something happens to it. The same goes for a diamond. Even when you grind up a solid into a powder, you will see little tiny pieces of that solid under a microscope. Liquids will move and fill up any container. Solids like their shape.
In the same way that a solid holds its shape, the atoms inside of a solid are not allowed to move around too much. This is one of the physical characteristics of solids. Atoms and molecules in liquids and gases are bouncing and floating around, free to move where they want. The molecules in a solid are stuck. The atoms still spin and the electrons fly around, but the entire atom will not change position.
Solids can be made up of many things. They can have pure elements or a variety of compounds inside. When you get more than one type of compound in a solid it is called a mixture. Most rocks are mixtures of many different compounds. Concrete is a good example of a manmade mixture.
CRYSTALS
On the other end of the spectrum from a mixture is something called a crystal. When a solid is made up of a pure substance and forms slowly, it can become a crystal. Not all pure substances form crystals because it is a delicate process. The atoms are arranged in a regular repeating pattern called a cystal lattice. A crystal lattice is a very exact organization of atoms. A good example is carbon. A diamond is a perfect crystal lattice while the graphite arrangement is more random.
LIQUID BASICS
The second state of matter we will discuss is a liquid. Solids are hard things you can hold. Gases are floating around you and in bubbles. What is a liquid? Water is a liquid. Your blood is a liquid. Liquids are an in-between state of matter. They can be found in between the solid and gas states. They don't have to be made up of the same compounds. If you have a variety of materials in a liquid, it is called a solution.
One characteristic of a liquid is that it will fill up the shape of a container. If you pour some water in a cup, it will fill up the bottom of the cup first and then fill the rest. The water will also take the shape of the cup. It fills the bottom first because of gravity. The top part of a liquid will usually have a flat surface. That flat surface is because of gravity too. Putting an ice cube (solid) into a cup will leave you with a cube in the middle of the cup; the shape won't change until the ice becomes a liquid.
Another trait of liquids is that they are difficult to compress. When you compress something, you take a certain amount and force it into a smaller space. Solids are very difficult to compress and gases are very easy. Liquids are in the middle but tend to be difficult. When you compress something, you force the atoms closer together. When pressure go up, substances are compressed. Liquids already have their atoms close together, so they are hard to compress. Many shock absorbers in cars compress liquids in tubes.
A special force keeps liquids together. Solids are stuck together and you have to force them apart. Gases bounce everywhere and they try to spread themselves out. Liquids actually want to stick together. There will always be the occasional evaporation where extra energy gets a molecule excited and the molecule leaves the system. Overall, liquids have cohesive (sticky) forces at work that hold the molecules together.
LOOKING FOR A GAS
Gas is everywhere. There is something called the atmosphere. That's a big layer of gas that surrounds the Earth. Gases are random groups of atoms. In solids, atoms and molecules are compact and close together. Liquids have atoms a little more spread out. However, gases are really spread out and the atoms and molecules are full of energy. They are bouncing around constantly.
Gases can fill a container of any size or shape. That is one of their physical characteristics. Think about a balloon. No matter what shape you make the balloon it will be evenly filled with the gas atoms. The atoms and molecules are spread equally throughout the entire balloon. Liquids can only fill the bottom of the container while gases can fill it entirely.
You might hear the term vapor. Vapor and gas mean the same thing. The word vapor is used to describe gases that are usually found as liquids. Good examples are water or mercury (Hg). Compounds like carbon dioxide are usually gases at room temperature so scientists will rarely talk about carbon dioxide vapor. Water and mercury are liquids at room temperature so they get the vapor title.
Gases hold huge amounts of energy, and their molecules are spread out as much as possible. With very little pressure, when compared to liquids and solids, those molecules can be compressed. It happens all of the time. Combinations of pressure and decreasing temperature force gases into tubes that we use every day. You might see compressed air in a spray bottle or feel the carbon dioxide rush out of a can of soda. Those are both examples of gas forced into a space smaller than it would want, and the gas escapes the first chance it gets.
PLASMA BASICS
Plasmas are a lot like gases, but the atoms are different because they are made up of free electrons and ions of the element. You don't find plasmas too often when you walk around. They aren't things that happen regularly on Earth. If you have ever heard of the Northern Lights or ball lightning, you might know that those are types of plasmas. It takes a very special environment to keep plasmas going. They are different and unique from the other states of matter.
FINDING A PLASMA
You won't find plasmas just anywhere. However, there may be some in front of you. Think about a fluorescent light bulb. They are not like regular light bulbs. Inside the long tube is a gas. Electricity flows through the tube when the light is turned on. The electricity acts as that special energy and charges up the gas. This charging and exciting of the atoms creates glowing plasma inside the bulb.
Another example of plasma is a neon sign. Just like a fluorescent light, neon signs are glass tubes filled with gas. When the light is turned on, the electricity flows through the tube. The electricity charges the gas, possibly neon, and creates plasma inside of the tube. The plasma glows a special color depending on what kind of gas is inside.
You also see plasma when you look at stars. Stars are big balls of gases at really high temperatures. The high temperatures charge up the atoms and create plasma. Stars are another good example of how the temperature of plasmas can be very different. Fluorescent lights are cold compared to really hot stars. They are still both forms of plasma, even with different physical characteristics.
BOSE-EINSTEIN BASICS
This state of matter was the only one created while you were alive. In 1995, two scientists, Cornell and Weiman, finally created this new state of matter. Two other scientists, Satyendra Bose and Albert Einstein, had predicted it in the 1920. They didn't have the equipment and facilities to make it happen in the 20s. Now we do. If plasmas are super hot and super excited atoms, the atoms in a Bose-Einstein condensate (BEC) are total opposites. They are super-unexcited and super-cold atoms.
ABOUT CONDENSATION
Let's explain condensation first. Condensation happens when several gas molecules come together and form a liquid. It all happens because of a loss of energy. Gases are really excited atoms. When they lose energy, they slow down and begin to collect. They can collect into one drop. Water condenses on the lid of your pot when you boil water. It cools on the metal and becomes a liquid again. You would then have a condensate.
The BEC happens at super low temperatures. We have talked about temperature scales and Kelvin. At zero Kelvin all molecular motion stops. Scientists have figured out a way to get a temperature only a few billionths of a degree above absolute zero. When temperatures get that low, you can create a BEC with a few special elements. Cornell and Weiman did it with Rubidium.
LET THE CLUMPING BEGIN
So it's cold. A cold ice cube is still a solid. When you get to a temperature near absolute zero something special happens. Atoms begin to clump. The whole process happens at temperatures within a few billionths of a degree so you won't see this at home. The result of this clumping is the BEC. A group of atoms takes up the same place, creating a "super atom." There are no longer thousands of separate atoms. They all take on the same qualities and for our purposes become one blob.Phase transition
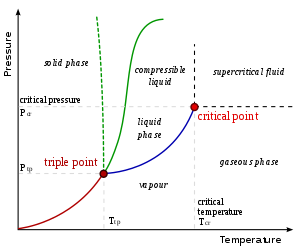
In thermodynamics, a phase transition is the transformation of a thermodynamic system from one phase to another.
At phase-transition point, physical properties may undergo abrupt change- for instance, volume of the two phases may be vastly different. As an example imagine transition of liquid water into vapour at boiling point.
In the English vernacular, the term is most commonly used to describe transitions between solid, liquid and gaseous states of matter, in rare cases including plasma.
Contents |
Types of phase transition
Examples of phase transitions include:
- The transitions between the solid, liquid, and gaseous phases of a single component, due to the effects of temperature and/or pressure
-
- (see also vapor pressure and phase diagram)
- A eutectic transformation, in which a two component single phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation.
- A peritectic transformation, in which a two component single phase solid is heated and transforms into a solid phase and a liquid phase.
- A spinodal decomposition, in which a single phase is cooled and separates into two different compositions of that same phase.
- The transition between the ferromagnetic and paramagnetic phases of magnetic materials at the Curie point.
- The transition between differently ordered, commensurate or incommensurate, magnetic structures, such as in cerium antimonide.
- The martensitic transformation which occurs as one of the many phase transformations in carbon steel and stands as a model for displacive phase transformations.
- Changes in the crystallographic structure such as between ferrite and austenite of iron.
- Order-disorder transitions such as in alpha-titanium aluminides.
- The emergence of superconductivity in certain metals when cooled below a critical temperature.
- The transition between different molecular structures (polymorphs or allotropes), especially of solids, such as between an amorphous structure and a crystal structure or between two different crystal structures.
- Quantum condensation of bosonic fluids, such as Bose-Einstein condensation and the superfluid transition in liquid helium.
- The breaking of symmetries in the laws of physics during the early history of the universe as its temperature cooled.
- Phase transitions in intractable computational complexity problems such as NP-complete or PSPACE problems. For example it has been noticed in k-SAT problems that the transition from solvable to unsolvable instances exhibits threshold behavior depending on the ratio of number of clauses to number of variables. Moreover, the amount of computational time required to solve the problem or determine it to be unsolvable increases drastically around the threshold. This line of research comes mostly from investigating similarities between computational complexity and statistical physics.
Phase transitions happen when the free energy of a system is non-analytic for some choice of thermodynamic variables - see phases. This non-analyticity generally stems from the interactions of an extremely large number of particles in a system, and does not appear in systems that are too small.
To put it simply, at phase-transition point (for instance, boiling point for water) the two phases of water - liquid and vapour have identical free energies and therefore are equally likely to exist. Below the boiling point, liquid-water is more stable state of the two. At boiling point liquid and vapour are equally stable and above boiling point vapour is more stable than liquid state of water.
It is sometimes possible to change the state of a system non-adiabatically in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable i.e. not theoretically stable, but quasistable. See superheating, supercooling and supersaturation.
Magnetic phases
Often also magnetic phases are used as the basis of a theory, and for introductory motivation. However, usually these are similar to the well-known liquid (
ferromagnetic) or gaseous ( paramagnetic) phases, as can be seen by the two equivalent interpretations, the magnetic one ("up" or "down" spins) or the lattice-gas interpretation ("occupied" or "unoccupied" sites) of a prominent binary model, the Ising model.
Therefore we can adhere to the above table of examples.
Classification of phase transitions
Ehrenfest classification
The first attempt at classifying phase transitions was the Ehrenfest classification scheme, which grouped phase transitions based on the degree of non-analyticity involved.
In other words, even though the chemical potential of the component undergoing phase transition remains unchanged, its derivative with respect to a state variable (for instance temperature) changes. The nature of this change is the basis of Ehrenfest classification scheme.
Though useful, Ehrenfest's classification is flawed, as will be discussed in the next section.
Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with a thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density (which is the first derivative of the free energy with respect to chemical potential.) Second-order phase transitions are continuous in the first derivative but exhibit discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.
Modern classification of phase transitions
The Ehrenfest scheme is an inaccurate method of classifying phase transitions, for it does not take into account the case where a derivative of free energy diverges (which is only possible in the thermodynamic limit). For instance, in the ferromagnetic transition, the heat capacity diverges to infinity.
In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:
The first-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy. During this process, the temperature of the system will stay constant as heat is added.
Because energy cannot be instantaneously transferred between the system and its environment, first-order transitions are associated with "mixed-phase regimes" in which some parts of the system have completed the transition and others have not. This phenomenon is familiar to anyone who has boiled a pot of water: the water does not instantly turn into gas, but forms a turbulent mixture of water and water vapor bubbles. Mixed-phase systems are difficult to study, because their dynamics are violent and hard to control. However, many important phase transitions fall in this category, including the solid/liquid/gas transitions and Bose-Einstein condensation.
The second class of phase transitions are the continuous phase transitions, also called second-order phase transitions. These have no associated latent heat. Examples of second-order phase transitions are the ferromagnetic transition, superconductor and the superfluid transition. Lev Landau gave a phenomenological theory of second order phase transitions.
An example of such a second-order phase transition is the glass transition of polymeric materials which occurs at glass transition temperature Tg of the polymer, and that is the reason why Tg can be identified easily as a change in the slope of the heating energy vs. temperature curve that results from the measurement of Tg on Differential scanning calorimetry (DSC) while the first-order phase transition of melting point Tm looks as a clear peak on the same graph.
Several transitions are known as the infinite-order phase transitions. They are continuous but break no symmetries. The most famous example is the Kosterlitz-Thouless transition in the two-dimensional XY model. Many quantum phase transitions in two-dimensional electron gases belong to this class.
Properties of phase transitions
Critical points
In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent.
This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid, due to density fluctuations at all possible wavelengths (including those of visible light).
Symmetry
Phase transitions often (but not always) take place between phases with different symmetry. Consider, for example, the transition between a fluid (i.e. liquid or gas) and a crystalline solid. A fluid, which is composed of atoms arranged in a disordered but homogeneous manner, possesses continuous translational symmetry: each point inside the fluid has the same properties as any other point. A crystalline solid, on the other hand, is made up of atoms arranged in a regular lattice. Each point in the solid is not similar to other points, unless those points are displaced by an amount equal to some lattice spacing.
Generally, we may speak of one phase in a phase transition as being more symmetrical than the other. The transition from the more symmetrical phase to the less symmetrical one is a symmetry-breaking process. In the fluid-solid transition, for example, we say that continuous translation symmetry is broken.
The ferromagnetic transition is another example of a symmetry-breaking transition, in this case the symmetry under reversal of the direction of electric currents and magnetic field lines. This symmetry is referred to as "up-down symmetry" or "time-reversal symmetry". It is broken in the ferromagnetic phase due to the formation of magnetic domains containing aligned magnetic moments. Inside each domain, there is a magnetic field pointing in a fixed direction chosen spontaneously during the phase transition. The name "time-reversal symmetry" comes from the fact that electric currents reverse direction when the time coordinate is reversed.
The presence of symmetry-breaking (or nonbreaking) is important to the behavior of phase transitions. It was pointed out by Landau that, given any state of a system, one may unequivocally say whether or not it possesses a given symmetry[citation needed]. Therefore, it cannot be possible to analytically deform a state in one phase into a phase possessing a different symmetry. This means, for example, that it is impossible for the solid-liquid phase boundary to end in a critical point like the liquid-gas boundary. However, symmetry-breaking transitions can still be either first- or second-order.
Typically, the more symmetrical phase is on the high-temperature side of a phase transition, and the less symmetrical phase on the low-temperature side. This is certainly the case for the solid-fluid and ferromagnetic transitions. This happens because the Hamiltonian of a system usually exhibits all the possible symmetries of the system, whereas the low-energy states lack some of these symmetries (this phenomenon is known as spontaneous symmetry breaking). At low temperatures, the system tends to be confined to the low-energy states. At higher temperatures, thermal fluctuations allow the system to access states in a broader range of energy, and thus more of the symmetries of the Hamiltonian.
Symmetries which are only present at low temperatures are called accidental symmetries. For example, a symmetry which is broken by a process which requires a lot of energy, such as the creation of heavy virtual particles, is an accidental symmetry at temperatures sufficiently low that this process is suppressed.
Order parameters
The order parameter is normally a quantity which is 0 in one phase, usually above the critical point and non-zero in the other. It characterises the onset of order at the phase transition. The order parameter susceptibility will usually diverge approaching the critical point. For a ferromagnetic system undergoing a phase transition, the order parameter is the net magnetization. For solid/liquid or liquid/gas transitions, it is the density.
When symmetry is broken, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. Such variables are examples of order parameters. An order parameter is a measure of the degree of order in a system; the extreme values are 0 for total disorder and 1 for complete order.[1] For example, an order parameter can indicate the degree of order in a liquid crystal. However, note that order parameters can also be defined for non-symmetry-breaking transitions.
There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.
Relevance for cosmology
Symmetry-breaking phase transitions play an important role in cosmology. It has been speculated that, in the hot early universe, the vacuum (i.e. the various quantum fields that fill space) possessed a large number of symmetries. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis.)
Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[2] and David Layzer [3]. See also Relational order theories.
- See also: order-disorder
Critical exponents and universality classes
Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.
It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc. When T is near Tc, the heat capacity C typically has a power law behaviour:
A similar behaviour, but with the exponent ν instead of α, applies for the correlation length.
The exponent ν is positive. This is different with α. Its actual value depends on the type of phase transition we are considering.
For -1 < α < href="http://en.wikipedia.org/wiki/Lambda_transition" title="Lambda transition">lambda transition from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003. At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample (see here). This experimental value of α agrees with theoretical predictions based on variational perturbation theory (see here).
For 0 < α < href="http://en.wikipedia.org/wiki/Ising_model" title="Ising model">Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ +0.110.
Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.
Several other critical exponents - β, γ, δ, ν, and η - are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations such as β = γ / (δ − 1), ν = γ / (2 − η). It can be shown that there are only two independent exponents, e.g. ν and η.
It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid-gas critical point have been found to be independent of the chemical composition of the fluid. More amazingly, but understandable from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergency of the correlation length is the essential point.
Critical slowing down and other phenomena
There are also other critical phenoma; e.g., besides static functions usually there is also the critical dynamics . As a consequence, at a phase transition one may observe critical slowing down or speeding up, respectively. As a consequence, the large static universality classes of a continuous phase transition split into smaller dynamic universality classes. Furthermore, in addition to the critical exponents there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.
Phase-change data storage
Several data-storage technologies use chalcogenide glass, which can be "switched" between two states, crystalline or amorphous, with the application of heat.
Phase change and optical disc technology
Phase change technology is also used to write to optical discs, such as CD-RW or DVD-RW discs. This is accomplished by including both a read laser and a more powerful write laser inside the drive. The discs contain a layer of a crystalline material that, when hit by a pulse of laser light from the write laser, changes to an amorphous state, thus changing its reflectivity. A different pulse level will reverse the changes, thus erasing the recorded information. The read laser is not powerful enough to induce a phase change, but can be used by the drive to tell whether a bit is "on" or "off" based on an area of the disc's reflectivity.
History of phase change optical disc technology
- 1990: LF 7010 by Panasonic, store 472 MB per side.
- 1995: PD (Phasewriter Dual) by Panasonic, store 650 MB.
- 1996: CD-RW (Compact Disc ReWritable) by Philips, Sony, Hewlett-Packard, Mitsubishi Chemical Corp. and Ricoh, store initially 650 MB and later 700 MB.
- 1998: DVD-RAM (DVD-Random Access Memory) by Panasonic, store initially 2.6 GB and later 4.7 GB.
- 199x: DVD±RW (DVD-ReWritable) by supplier consortium, store 4.7 GB.
- 2004: PDD (Professional Disc for Data) by Sony, store 20.5 GB.
- 2004: UDO (Ultra Density Optical) by Plasmon, store 28 GB.
- 2006: BD-RE (Blu-ray Disc Rerecordable) by Sony, store 50 GB.
Phase-change memory
Phase-change memory (PRAM) is a kind of non-volatile computer memory. Prototype PRAM devices have demonstrated higher density and faster write times than flash memory.
PRAM uses chalcogenide glass, the same material utilized in re-writable optical media (such as CD-RW and DVD-RW). The amorphous, high resistance state is used to represent a binary 1, and the crystalline, low resistance state represents a 0.
Samsung, Intel, and STMicroelectronics demonstrated prototype PRAM devices in 2006, and announced plans for commercial productions.
No comments:
Post a Comment