History of physics
Physics is the science of matter and its behaviour and motion. It is one of the oldest scientific disciplines, perhaps the oldest through its inclusion of astronomy. The first written work of physics with that title was Aristotle's Physics.
Elements of what became physics were drawn primarily from the fields of astronomy, optics, and mechanics, which were methodologically united through the study of geometry. These disciplines began in Antiquity with the Babylonians and with Hellenistic writers such as Archimedes and Ptolemy, then passed on to the Arabic-speaking world where they were critiqued and developed into a more physical and experimental tradition by scientists such as Ibn al-Haytham and Abū Rayhān Bīrūnī,[1][2] before eventually passing on to Western Europe where they were studied by scholars such as Roger Bacon and Witelo. They were thought of as technical in character and many philosophers generally did not perceive their descriptive content as representing a philosophically significant knowledge of the natural world. Similar mathematical traditions also existed in ancient Chinese and Indian sciences.
Meanwhile, philosophy, including what was called “physics”, focused on explanatory (rather than descriptive) schemes developed around the Aristotelian idea of the four types of “causes”. According to Aristotelian and, later, Scholastic physics, things moved in the way that they did because it was part of their essential nature to do so. Celestial objects were thought to move in circles, because perfect circular motion was considered an innate property of objects that existed in the uncorrupted realm of the celestial spheres. The theory of impetus, the ancestor to the concepts of inertia and momentum, also belonged to this philosophical tradition, and was developed by medieval philosophers such as John Philoponus, Avicenna and Jean Buridan. The physical traditions in ancient China and India were also largely philosophical.
In the philosophical tradition of "physics", motions below the lunar sphere were seen as imperfect, and thus could not be expected to exhibit consistent motion. More idealized motion in the “sublunary” realm could only be achieved through artifice, and prior to the 17th century, many philosophers did not view artificial experiments as a valid means of learning about the natural world. Instead, physical explanations in the sublunary realm revolved around tendencies. Stones contained the element earth, and earthy objects tended to move in a straight line toward the center of the universe (which the earth was supposed to be situated around) unless otherwise prevented from doing so. Other physical explanations, which would not later be considered within the bounds of physics, followed similar reasoning. For instance, people tended to think, because people were, by their essential nature, thinking animals.
- Further information: History of astronomy and Aristotelian physics
Emergence of experimental method and physical optics
The use of experiments in the sense of empirical procedures[3] in geometrical optics dates back to second century Roman Egypt, where Ptolemy carried out several early such experiments on reflection, refraction and binocular vision.[4] Due to his Platonic methodological paradigm of "saving the appearances", however, he discarded or rationalized any empirical data that did not support his theories,[5] as the idea of experiment did not hold any importance in Antiquity.[6] The incorrect emission theory of vision thus continued to dominate optics through to the 10th century.

The turn of the second millennium saw the emergence of experimental physics with the development of an experimental method emphasizing the role of experimentation as a form of proof in scientific inquiry, and the development of physical optics where the mathematical discipline of geometrical optics was successfully unified with the philosophical field of physics. The Iraqi physicist, Ibn al-Haytham (Alhazen), is considered a central figure in this shift in physics from a philosophical activity to an experimental and mathematical one, and the shift in optics from a mathematical discipline to a physical and experimental one.[7][8][9][10][11][12] Due to his positivist approach,[13] his Doubts Concerning Ptolemy insisted on scientific demonstration and criticized Ptolemy's confirmation bias and conjectural undemonstrated theories.[14] His Book of Optics (1021) was the earliest successful attempt at unifying a mathematical discipline (geometrical optics) with the philosophical field of physics, to create the modern science of physical optics. An important part of this was the intromission theory of vision, which in order to prove, he developed an experimental method to test his hypothesis.[7][8][9][10][12][15] He conducted various experiments to prove his intromission theory[16] and other hypotheses on light and vision.[17] The Book of Optics established experimentation as the norm of proof in optics,[15] and gave optics a physico-mathematical conception at a much earlier date than the other mathematical disciplines.[18] His On the Light of the Moon also attempted to combine mathematical astronomy with physics, a field now known as astrophysics, to formulate several astronomical hypotheses which he proved through experimentation.[9]
Galileo Galilei and the rise of physico-mathematics

In the 17th century, natural philosophers began to mount a sustained attack on the Scholastic philosophical program, and supposed that mathematical descriptive schemes adopted from such fields as mechanics and astronomy could actually yield universally valid characterizations of motion. The Tuscan mathematician Galileo Galilei was the central figure in the shift to this perspective. As a mathematician, Galileo’s role in the university culture of his era was subordinated to the three major topics of study: law, medicine, and theology (which was closely allied to philosophy). Galileo, however, felt that the descriptive content of the technical disciplines warranted philosophical interest, particularly because mathematical analysis of astronomical observations—notably the radical analysis offered by astronomer Nicolaus Copernicus concerning the relative motions of the sun, earth, moon, and planets—indicated that philosophers’ statements about the nature of the universe could be shown to be in error. Galileo also performed mechanical experiments, and insisted that motion itself—regardless of whether that motion was natural or artificial—had universally consistent characteristics that could be described mathematically.
Galileo used his 1609 telescopic discovery of the moons of Jupiter, as published in his Sidereus Nuncius in 1610, to procure a position in the Medici court with the dual title of mathematician and philosopher. As a court philosopher, he was expected to engage in debates with philosophers in the Aristotelian tradition, and received a large audience for his own publications, such as The Assayer and Discourses and Mathematical Demonstrations Concerning Two New Sciences, which was published abroad after he was placed under house arrest for his publication of Dialogue Concerning the Two Chief World Systems in 1632.[19][20]
Galileo’s interest in the mechanical experimentation and mathematical description in motion established a new natural philosophical tradition focused on experimentation. This tradition, combining with the non-mathematical emphasis on the collection of "experimental histories" by philosophical reformists such as William Gilbert and Francis Bacon, drew a significant following in the years leading up to and following Galileo’s death, including Evangelista Torricelli and the participants in the Accademia del Cimento in Italy; Marin Mersenne and Blaise Pascal in France; Christiaan Huygens in the Netherlands; and Robert Hooke and Robert Boyle in England.
The Cartesian philosophy of motion

The French philosopher René Descartes was well-connected to, and influential within, the experimental philosophy networks. Descartes had a more ambitious agenda, however, which was geared toward replacing the Scholastic philosophical tradition altogether. Questioning the reality interpreted through the senses, Descartes sought to reestablish philosophical explanatory schemes by reducing all perceived phenomena to being attributable to the motion of an invisible sea of “corpuscles”. (Notably, he reserved human thought and God from his scheme, holding these to be separate from the physical universe). In proposing this philosophical framework, Descartes supposed that different kinds of motion, such as that of planets versus that of terrestrial objects, were not fundamentally different, but were merely different manifestations of an endless chain of corpuscular motions obeying universal principles. Particularly influential were his explanation for circular astronomical motions in terms of the vortex motion of corpuscles in space (Descartes argued, in accord with the beliefs, if not the methods, of the Scholastics, that a vacuum could not exist), and his explanation of gravity in terms of corpuscles pushing objects downward.[21][22][23]
- Further information: Mechanical explanations of gravitation
Descartes, like Galileo, was convinced of the importance of mathematical explanation, and he and his followers were key figures in the development of mathematics and geometry in the 17th century. Cartesian mathematical descriptions of motion held that all mathematical formulations had to be justifiable in terms of direct physical action, a position held by Huygens and the German philosopher Gottfried Leibniz, who, while following in the Cartesian tradition, developed his own philosophical alternative to Scholasticism, which he outlined in his 1714 work, The Monadology.
Newtonian motion versus Cartesian motion

In the late 17th and early 18th centuries, the Cartesian mechanical tradition was challenged by another philosophical tradition established by the Cambridge University mathematician Isaac Newton. Where Descartes held that all motions should be explained with respect to the immediate force exerted by corpuscles, Newton chose to describe universal motion with reference to a set of fundamental mathematical principles: his three laws of motion and the law of gravitation, which he introduced in his 1687 work Mathematical Principles of Natural Philosophy. Using these principles, Newton removed the idea that objects followed paths determined by natural shapes (such as Kepler’s idea that planets moved naturally in ellipses), and instead demonstrated that not only regularly observed paths, but all the future motions of any body could be deduced mathematically based on knowledge of their existing motion, their mass, and the forces acting upon them. However, observed celestial motions did not precisely conform to a Newtonian treatment, and Newton, who was also deeply interested in theology, imagined that God intervened to ensure the continued stability of the solar system.

Newton’s principles (but not his mathematical treatments) proved controversial with Continental philosophers, who found his lack of metaphysical explanation for movement and gravitation philosophically unacceptable. Beginning around 1700, a bitter rift opened between the Continental and British philosophical traditions, which were stoked by heated, ongoing, and viciously personal disputes between the followers of Newton and Leibniz concerning priority over the analytical techniques of calculus, which each had developed independently. Initially, the Cartesian and Leibnizian traditions prevailed on the Continent (leading to the dominance of the Leibnizian calculus notation everywhere except Britain). Newton himself remained privately disturbed at the lack of a philosophical understanding of gravitation, while insisting in his writings that none was necessary to infer its reality. As the 18th century progressed, Continental natural philosophers increasingly accepted the Newtonians’ willingness to forgo ontological metaphysical explanations for mathematically described motions.[24][25][26]
Rational mechanics in the 18th century

The mathematical analytical traditions established by Newton and Leibniz flourished during the 18th century as more mathematicians learned calculus and elaborated upon its initial formulation. The application of mathematical analysis to problems of motion was known as rational mechanics, or mixed mathematics (and was later termed classical mechanics). This work primarily revolved around celestial mechanics, although other applications were also developed, such as the Swiss mathematician Daniel Bernoulli’s treatment of fluid dynamics, which he introduced in his 1738 work Hydrodynamica.[27]
Rational mechanics dealt primarily with the development of elaborate mathematical treatments of observed motions, using Newtonian principles as a basis, and emphasized improving the tractability of complex calculations and developing of legitimate means of analytical approximation. By the end of the century analytical treatments were rigorous enough to verify the stability of the solar system solely on the basis of Newton’s laws without reference to divine intervention—even as deterministic treatments of systems as simple as the three body problem in gravitation remained intractable.[28]
British work, carried on by mathematicians such as Brook Taylor and Colin Maclaurin, fell behind Continental developments as the century progressed. Meanwhile, work flourished at scientific academies on the Continent, led by such mathematicians as Daniel Bernoulli, Leonhard Euler, Joseph-Louis Lagrange, Pierre-Simon Laplace, and Adrien-Marie Legendre. At the end of the century, the members of the French Academy of Sciences had attained clear dominance in the field.[29][30][31][32]
Physical experimentation in the 18th and early 19th centuries
At the same time, the experimental tradition established by Galileo and his followers persisted. The Royal Society and the French Academy of Sciences were major centers for the performance and reporting of experimental work, and Newton was himself an influential experimenter, particularly in the field of optics, where he was recognized for his prism experiments dividing white light into its constituent spectrum of colors, as published in his 1704 book Opticks (which also advocated a particulate interpretation of light). Experiments in mechanics, optics, magnetism, static electricity, chemistry, and physiology were not clearly distinguished from each other during the 18th century, but significant differences in explanatory schemes and, thus, experiment design were emerging. Chemical experimenters, for instance, defied attempts to enforce a scheme of abstract Newtonian forces onto chemical affiliations, and instead focused on the isolation and classification of chemical substances and reactions.[33]
Nevertheless, the separate fields remained tied together, most clearly through the theories of weightless “imponderable fluids", such as heat (“caloric”), electricity, and phlogiston (which was rapidly overthrown as a concept following Lavoisier’s identification of oxygen gas late in the century). Assuming that these concepts were real fluids, their flow could be traced through a mechanical apparatus or chemical reactions. This tradition of experimentation led to the development of new kinds of experimental apparatus, such as the Leyden Jar and the Voltaic Pile; and new kinds of measuring instruments, such as the calorimeter, and improved versions of old ones, such as the thermometer. Experiments also produced new concepts, such as the University of Glasgow experimenter Joseph Black’s notion of latent heat and Philadelphia intellectual Benjamin Franklin’s characterization of electrical fluid as flowing between places of excess and deficit (a concept later reinterpreted in terms of positive and negative charges).

While it was recognized early in the 18th century that finding absolute theories of electrostatic and magnetic force akin to Newton’s principles of motion would be an important achievement, none were forthcoming. This impossibility only slowly disappeared as experimental practice became more widespread and more refined in the early years of the 19th century in places such as the newly-established Royal Institution in London, where John Dalton argued for an atomistic interpretation of chemistry, Thomas Young argued for the interpretation of light as a wave, and Michael Faraday established the phenomenon of electromagnetic induction. Meanwhile, the analytical methods of rational mechanics began to be applied to experimental phenomena, most influentially with the French mathematician Joseph Fourier’s analytical treatment of the flow of heat, as published in 1822.[34][35][36]
Thermodynamics, statistical mechanics, and electromagnetic theory

The establishment of a mathematical physics of energy between the 1850s and the 1870s expanded substantially on the physics of prior eras and challenged traditional ideas about how the physical world worked. While Pierre-Simon Laplace’s work on celestial mechanics solidified a deterministically mechanistic view of objects obeying fundamental and totally reversible laws, the study of energy and particularly the flow of heat, threw this view of the universe into question. Drawing upon the engineering theory of Lazare and Sadi Carnot, and Émile Clapeyron; the experimentation of James Prescott Joule on the interchangeability of mechanical, chemical, thermal, and electrical forms of work; and his own Cambridge mathematical tripos training in mathematical analysis; the Glasgow physicist William Thomson and his circle of associates established a new mathematical physics relating to the exchange of different forms of energy and energy’s overall conservation (what is still accepted as the “first law of thermodynamics”). Their work was soon allied with the theories of similar but less-known work by the German physician Julius Robert von Mayer and physicist and physiologist Hermann von Helmholtz on the conservation of forces.

Taking his mathematical cues from the heat flow work of Joseph Fourier (and his own religious and geological convictions), Thomson believed that the dissipation of energy with time (what is accepted as the “second law of thermodynamics”) represented a fundamental principle of physics, which was expounded in Thomson and Peter Guthrie Tait’s influential work Treatise on Natural Philosophy. However, other interpretations of what Thomson called thermodynamics were established through the work of the German physicist Rudolf Clausius. His statistical mechanics, which was elaborated upon by Ludwig Boltzmann and the British physicist James Clerk Maxwell, held that energy (including heat) was a measure of the speed of particles. Interrelating the statistical likelihood of certain states of organization of these particles with the energy of those states, Clausius reinterpreted the dissipation of energy to be the statistical tendency of molecular configurations to pass toward increasingly likely, increasingly disorganized states (coining the term “entropy” to describe the disorganization of a state). The statistical versus absolute interpretations of the second law of thermodynamics set up a dispute that would last for several decades (producing arguments such as “Maxwell's demon”), and that would not be held to be definitively resolved until the behavior of atoms was firmly established in the early 20th century.[37][38]
- Further information: history of thermodynamics
Meanwhile, the new physics of energy transformed the analysis of electromagnetic phenomena, particularly through the introduction of the concept of the field and the publication of Maxwell’s 1873 Treatise on Electricity and Magnetism, which also drew upon theoretical work by German theoreticians such as Carl Friedrich Gauss and Wilhelm Weber. The encapsulation of heat in particulate motion, and the addition of electromagnetic forces to Newtonian dynamics established an enormously robust theoretical underpinning to physical observations. The prediction that light represented a transmission of energy in wave form through a “luminiferous ether”, and the seeming confirmation of that prediction with Helmholtz student Heinrich Hertz’s 1888 detection of electromagnetic radiation, was a major triumph for physical theory and raised the possibility that even more fundamental theories based on the field could soon be developed.[39][40][41][42] Research on the transmission of electromagnetic waves began soon after, with the experiments conducted by physicists such as Nikola Tesla, Jagadish Chandra Bose and Guglielmo Marconi during the 1890s leading to the invention of radio.
The emergence of a new physics circa 1900

The triumph of Maxwell’s theories was undermined by inadequacies that had already begun to appear. The Michelson-Morley experiment failed to detect a shift in the speed of light, which would have been expected as the earth moved at different angles with respect to the ether. The possibility explored by Hendrik Lorentz, that the ether could compress matter, thereby rendering it undetectable, presented problems of its own as a compressed electron (detected in 1897 by British experimentalist J. J. Thomson) would prove unstable. Meanwhile, other experimenters began to detect unexpected forms of radiation: Wilhelm Röntgen caused a sensation with his discovery of x-rays in 1895; in 1896 Henri Becquerel discovered that certain kinds of matter emit radiation on their own accord. Marie and Pierre Curie coined the term “radioactivity” to describe this property of matter, and isolated the radioactive elements radium and polonium. Ernest Rutherford and Frederick Soddy identified two of Becquerel’s forms of radiation with electrons and the element helium. In 1911 Rutherford established that the bulk of mass in atoms are concentrated in positively-charged nuclei with orbiting electrons, which was a theoretically unstable configuration. Studies of radiation and radioactive decay continued to be a preeminent focus for physical and chemical research through the 1930s, when the discovery of nuclear fission opened the way to the practical exploitation of what came to be called “atomic” energy.

Radical new physical theories also began to emerge in this same period. In 1905 Albert Einstein, then a Bern patent clerk, argued that the speed of light was a constant in all inertial reference frames and that electromagnetic laws should remain valid independent of reference frame—assertions which rendered the ether “superfluous” to physical theory, and that held that observations of time and length varied relative to how the observer was moving with respect to the object being measured (what came to be called the “special theory of relativity”). It also followed that mass and energy were interchangeable quantities according to the equation E=mc2. In another paper published the same year, Einstein asserted that electromagnetic radiation was transmitted in discrete quantities (“quanta”), according to a constant that the theoretical physicist Max Planck had posited in 1900 to arrive at an accurate theory for the distribution of blackbody radiation—an assumption that explained the strange properties of the photoelectric effect. The Danish physicist Niels Bohr used this same constant in 1913 to explain the stability of Rutherford’s atom as well as the frequencies of light emitted by hydrogen gas.
- Further information: History of special relativity
The radical years: general relativity and quantum mechanics
The gradual acceptance of Einstein’s theories of relativity and the quantized nature of light transmission, and of Niels Bohr’s model of the atom created as many problems as they solved, leading to a full-scale effort to reestablish physics on new fundamental principles. Expanding relativity to cases of accelerating reference frames (the “general theory of relativity”) in the 1910s, Einstein posited an equivalence between the inertial force of acceleration and the force of gravity, leading to the conclusion that space is curved and finite in size, and the prediction of such phenomena as gravitational lensing and the distortion of time in gravitational fields.
- Further information: History of general relativity

The quantized theory of the atom gave way to a full-scale quantum mechanics in the 1920s. The quantum theory (which previously relied in the “correspondence” at large scales between the quantized world of the atom and the continuities of the “classical” world) was accepted when the Compton Effect established that light carries momentum and can scatter off particles, and when Louis de Broglie asserted that matter can be seen as behaving as a wave in much the same way as electromagnetic waves behave like particles (wave-particle duality). New principles of a “quantum” rather than a “classical” mechanics, formulated in matrix-form by Werner Heisenberg, Max Born, and Pascual Jordan in 1925, were based on the probabilistic relationship between discrete “states” and denied the possibility of causality. Erwin Schrödinger established an equivalent theory based on waves in 1926; but Heisenberg’s 1927 “uncertainty principle” (indicating the impossibility of precisely and simultaneously measuring position and momentum) and the “Copenhagen interpretation” of quantum mechanics (named after Bohr’s home city) continued to deny the possibility of fundamental causality, though opponents such as Einstein would assert that “God does not play dice with the universe”.[43] Also in the 1920s, Satyendra Nath Bose's work on photons and quantum mechanics provided the foundation for Bose-Einstein statistics, the theory of the Bose-Einstein condensate, and the discovery of the boson.
- Further information: history of quantum mechanics
Constructing a new fundamental physics
As the philosophically inclined continued to debate the fundamental nature of the universe, quantum theories continued to be produced, beginning with Paul Dirac’s formulation of a relativistic quantum theory in 1927. However, attempts to quantize electromagnetic theory entirely were stymied throughout the 1930s by theoretical formulations yielding infinite energies. This situation was not considered adequately resolved until after World War II ended, when Julian Schwinger, Richard Feynman, and Sin-Itiro Tomonaga independently posited the technique of “renormalization”, which allowed for an establishment of a robust quantum electrodynamics (Q.E.D.).[44]
Meanwhile, new theories of fundamental particles proliferated with the rise of the idea of the quantization of fields through “exchange forces” regulated by an exchange of short-lived “virtual” particles, which were allowed to exist according to the laws governing the uncertainties inherent in the quantum world. Notably, Hideki Yukawa proposed that the positive charges of the nucleus were kept together courtesy of a powerful but short-range force mediated by a particle intermediate in mass between the size of an electron and a proton. This particle, called the “pion”, was identified in 1947, but it was part of a slew of particle discoveries beginning with the neutron, the “positron” (a positively-charged “antimatter” version of the electron), and the “muon” (a heavier relative to the electron) in the 1930s, and continuing after the war with a wide variety of other particles detected in various kinds of apparatus: cloud chambers, nuclear emulsions, bubble chambers, and coincidence counters. At first these particles were found primarily by the ionized trails left by cosmic rays, but were increasingly produced in newer and more powerful particle accelerators.[45]

The interaction of these particles by “scattering” and “decay” provided a key to new fundamental quantum theories. Murray Gell-Mann and Yuval Ne'eman brought some order to these new particles by classifying them according to certain qualities, beginning with what Gell-Mann referred to as the “Eightfold Way”, but proceeding into several different “octets” and “decuplets” which could predict new particles, most famously the Ω−, which was detected at Brookhaven National Laboratory in 1964, and which gave rise to the “quark” model of hadron composition. While the quark model at first seemed inadequate to describe strong nuclear forces, allowing the temporary rise of competing theories such as the S-Matrix, the establishment of quantum chromodynamics in the 1970s finalized a set of fundamental and exchange particles, which allowed for the establishment of a “standard model” based on the mathematics of gauge invariance, which successfully described all forces except for gravity, and which remains generally accepted within the domain to which it is designed to be applied.[46]
The “standard model” groups the electroweak interaction theory and quantum chromodynamics into a structure denoted by the gauge group SU(3)×SU(2)×U(1). The formulation of the unification of the electromagnetic and weak interactions in the standard model is due to Abdus Salam, Steven Weinberg and, subsequently, Sheldon Glashow. After the discovery, made at CERN, of the existence of neutral weak currents,[47][48][49][50] mediated by the Z boson foreseen in the standard model, the physicists Salam, Glashow and Weinberg received the 1979 Nobel Prize in Physics for their electroweak theory.[51]
While accelerators have confirmed most aspects of the standard model by detecting expected particle interactions at various collision energies, no theory reconciling the general theory of relativity with the standard model has yet been found, although “string theory” has provided one promising avenue forward. Since the 1970s, fundamental particle physics has provided insights into early universe cosmology, particularly the “big bang” theory proposed as a consequence of Einstein’s general theory. However, starting from the 1990s, astronomical observations have also provided new challenges, such as the need for new explanations of galactic stability (the problem of dark matter), and accelerating expansion of the universe (the problem of dark energy).
The physical sciences
With increased accessibility to and elaboration upon advanced analytical techniques in the 19th century, physics was defined as much, if not more, by those techniques than by the search for universal principles of motion and energy, and the fundamental nature of matter. Fields such as acoustics, geophysics, astrophysics, aerodynamics, plasma physics, low-temperature physics, and solid-state physics joined optics, fluid dynamics, electromagnetism, and mechanics as areas of physical research. In the 20th century, physics also became closely allied with such fields as electrical, aerospace, and materials engineering, and physicists began to work in government and industrial laboratories as much as in academic settings. Following World War II, the population of physicists increased dramatically, and came to be centered on the United States, while, in more recent decades, physics has become a more international pursuit than at any time in its previous history.
Classical mechanics
| Classical mechanics | ||||
History of ...
| ||||
Classical mechanics is used for describing the motion of macroscopic objects, from projectiles to parts of machinery, as well as astronomical objects, such as spacecraft, planets, stars, and galaxies. It produces very accurate results within these domains, and is one of the oldest and largest subjects in science, engineering and technology.
Besides this, many related specialties exist, dealing with gases, liquids, and solids, and so on. Classical mechanics is enhanced by special relativity for objects moving with high velocity, approaching the speed of light; general relativity is employed to handle gravitation at a deeper level; and quantum mechanics handles the wave-particle duality of atoms and molecules.
In physics, classical mechanics is one of the two major sub-fields of study in the science of mechanics, which is concerned with the set of physical laws governing and mathematically describing the motions of bodies and aggregates of bodies. The other sub-field is quantum mechanics.
The term classical mechanics was coined in the early 20th century to describe the system of mathematical physics begun by Isaac Newton and many contemporary 17th century workers, building upon the earlier astronomical theories of Johannes Kepler, which in turn were based on the precise observations of Tycho Brahe and the studies of terrestrial projectile motion of Galileo, but before the development of quantum physics and relativity. Therefore, some sources exclude so-called "relativistic physics" from that category. However, a number of modern sources do include Einstein's mechanics, which in their view represents classical mechanics in its most developed and most accurate form. The initial stage in the development of classical mechanics is often referred to as Newtonian mechanics, and is associated with the physical concepts employed by and the mathematical methods invented by Newton himself, in parallel with Leibniz, and others. This is further described in the following sections. More abstract and general methods include Lagrangian mechanics and Hamiltonian mechanics. Much of the content of classical mechanics was created in the 18th and 19th centuries and extends considerably beyond (particularly in its use of analytical mathematics) the work of Newton.
Contents |
Description of the theory
The following introduces the basic concepts of classical mechanics. For simplicity, it often models real-world objects as point particles, objects with negligible size. The motion of a point particle is characterized by a small number of parameters: its position, mass, and the forces applied to it. Each of these parameters is discussed in turn.
In reality, the kind of objects which classical mechanics can describe always have a non-zero size. (The physics of very small particles, such as the electron, is more accurately described by quantum mechanics). Objects with non-zero size have more complicated behavior than hypothetical point particles, because of the additional degrees of freedom—for example, a baseball can spin while it is moving. However, the results for point particles can be used to study such objects by treating them as composite objects, made up of a large number of interacting point particles. The center of mass of a composite object behaves like a point particle.
[edit] Displacement and its derivatives
| The SI derived units with kg, m and s | |
| displacement | m |
| speed | m s−1 |
| acceleration | m s−2 |
| jerk | m s−3 |
| specific energy | m² s−2 |
| absorbed dose rate | m² s−3 |
| moment of inertia | kg m² |
| momentum | kg m s−1 |
| angular momentum | kg m² s−1 |
| force | kg m s−2 |
| torque | kg m² s−2 |
| energy | kg m² s−2 |
| power | kg m² s−3 |
| pressure | kg m−1 s−2 |
| surface tension | kg s−2 |
| irradiance | kg s−3 |
| kinematic viscosity | m² s−1 |
| dynamic viscosity | kg m−1 s |
The displacement, or position, of a point particle is defined with respect to an arbitrary fixed reference point, O, in space, usually accompanied by a coordinate system, with the reference point located at the origin of the coordinate system. It is defined as the vector r from O to the particle. In general, the point particle need not be stationary relative to O, so r is a function of t, the time elapsed since an arbitrary initial time. In pre-Einstein relativity (known as Galilean relativity), time is considered an absolute, i.e., the time interval between any given pair of events is the same for all observers. In addition to relying on absolute time, classical mechanics assumes Euclidean geometry for the structure of space.[1]
[edit] Velocity and speed
The velocity, or the rate of change of position with time, is defined as the derivative of the position with respect to time or
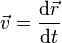 .
.
In classical mechanics, velocities are directly additive and subtractive. For example, if one car traveling East at 60 km/h passes another car traveling East at 50 km/h, then from the perspective of the slower car, the faster car is traveling east at 60 − 50 = 10 km/h. Whereas, from the perspective of the faster car, the slower car is moving 10 km/h to the West. Velocities are directly additive as vector quantities; they must be dealt with using vector analysis.
Mathematically, if the velocity of the first object in the previous discussion is denoted by the vector 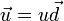 and the velocity of the second object by the vector
and the velocity of the second object by the vector  where u is the speed of the first object, v is the speed of the second object, and
where u is the speed of the first object, v is the speed of the second object, and  and
and  are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is:
are unit vectors in the directions of motion of each particle respectively, then the velocity of the first object as seen by the second object is:
Similarly:
When both objects are moving in the same direction, this equation can be simplified to:
Or, by ignoring direction, the difference can be given in terms of speed only:
[edit] Acceleration
The acceleration, or rate of change of velocity, is the derivative of the velocity with respect to time (the second derivative of the position with respect to time) or
 .
.
Acceleration can arise from a change with time of the magnitude of the velocity or of the direction of the velocity or both. If only the magnitude, v, of the velocity decreases, this is sometimes referred to as deceleration, but generally any change in the velocity with time, including deceleration, is simply referred to as acceleration.
Frames of reference
While the position and velocity and acceleration of a particle can be referred to any observer in any state of motion, classical mechanics assumes the existence of a special family of reference frames in terms of which the mechanical laws of nature take a comparatively simple form. These special reference frames are called inertial frames. They are characterized by the absence of acceleration of the observer and the requirement that all forces entering the observer's physical laws originate in identifiable sources (charges, gravitational bodies, and so forth). A non-inertial reference frame is one accelerating with respect to an inertial one, and in such a non-inertial frame a particle is subject to acceleration by fictitious forces that enter the equations of motion solely as a result of its accelerated motion, and do not originate in identifiable sources. These fictitious forces are in addition to the real forces recognized in an inertial frame. A key concept of inertial frames is the method for identifying them. (See inertial frame of reference for a discussion.) For practical purposes, reference frames that are unaccelerated with respect to the distant stars are regarded as good approximations to inertial frames.
The following consequences can be derived about the perspective of an event in two inertial reference frames, S and S', where S' is traveling at a relative velocity of 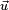 to S.
to S.
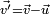 (the velocity
(the velocity 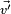 of a particle from the perspective of S' is slower by
of a particle from the perspective of S' is slower by 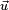 than its velocity
than its velocity  from the perspective of S)
from the perspective of S)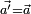 (the acceleration of a particle remains the same regardless of reference frame)
(the acceleration of a particle remains the same regardless of reference frame)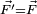 (the force on a particle remains the same regardless of reference frame)
(the force on a particle remains the same regardless of reference frame)- the speed of light is not a constant in classical mechanics, nor does the special position given to the speed of light in relativistic mechanics have a counterpart in classical mechanics.
- the form of Maxwell's equations is not preserved across such inertial reference frames. However, in Einstein's theory of special relativity, the assumed constancy (invariance) of the vacuum speed of light alters the relationships between inertial reference frames so as to render Maxwell's equations invariant.
Forces; Newton's Second Law
Newton was the first to mathematically express the relationship between force and momentum. Some physicists interpret Newton's second law of motion as a definition of force and mass, while others consider it to be a fundamental postulate, a law of nature. Either interpretation has the same mathematical consequences, historically known as "Newton's Second Law":
 .
.
The quantity  is called the (canonical) momentum. The net force on a particle is, thus, equal to rate change of momentum of the particle with time. Since the definition of acceleration is
is called the (canonical) momentum. The net force on a particle is, thus, equal to rate change of momentum of the particle with time. Since the definition of acceleration is  , when the mass of the object is fixed, for example, when the mass variation with velocity found in special relativity is negligible (an implicit approximation in Newtonian mechanics), Newton's law can be written in the simplified and more familiar form
, when the mass of the object is fixed, for example, when the mass variation with velocity found in special relativity is negligible (an implicit approximation in Newtonian mechanics), Newton's law can be written in the simplified and more familiar form
 .
.
So long as the force acting on a particle is known, Newton's second law is sufficient to describe the motion of a particle. Once independent relations for each force acting on a particle are available, they can be substituted into Newton's second law to obtain an ordinary differential equation, which is called the equation of motion.
As an example, assume that friction is the only force acting on the particle, and that it may be modeled as a function of the velocity of the particle, for example:
with λ a positive constant.. Then the equation of motion is
 .
.
This can be integrated to obtain
where 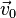 is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy), slowing it down. This expression can be further integrated to obtain the position
is the initial velocity. This means that the velocity of this particle decays exponentially to zero as time progresses. In this case, an equivalent viewpoint is that the kinetic energy of the particle is absorbed by friction (which converts it to heat energy in accordance with the conservation of energy), slowing it down. This expression can be further integrated to obtain the position 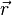 of the particle as a function of time.
of the particle as a function of time.
Important forces include the gravitational force and the Lorentz force for electromagnetism. In addition, Newton's third law can sometimes be used to deduce the forces acting on a particle: if it is known that particle A exerts a force 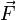 on another particle B, it follows that B must exert an equal and opposite reaction force, -
on another particle B, it follows that B must exert an equal and opposite reaction force, -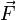 , on A. The strong form of Newton's third law requires that
, on A. The strong form of Newton's third law requires that 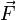 and -
and -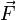 act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
act along the line connecting A and B, while the weak form does not. Illustrations of the weak form of Newton's third law are often found for magnetic forces.
Energy
If a force 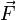 is applied to a particle that achieves a displacement
is applied to a particle that achieves a displacement  , the work done by the force is defined as the scalar product of force and displacement vectors:
, the work done by the force is defined as the scalar product of force and displacement vectors:
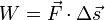 .
.
If the mass of the particle is constant, and Wtotal is the total work done on the particle, obtained by summing the work done by each applied force, from Newton's second law:
 ,
,
where Ek is called the kinetic energy. For a point particle, it is mathematically defined as the amount of work done to accelerate the particle from zero velocity to the given velocity v:
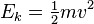 .
.
For extended objects composed of many particles, the kinetic energy of the composite body is the sum of the kinetic energies of the particles.
A particular class of forces, known as conservative forces, can be expressed as the gradient of a scalar function, known as the potential energy and denoted Ep:
 .
.
If all the forces acting on a particle are conservative, and Ep is the total potential energy (which is defined as a work of involved forces to rearrange mutual positions of bodies), obtained by summing the potential energies corresponding to each force
|
| 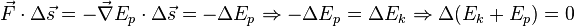 . . |
This result is known as conservation of energy and states that the total energy,
is constant in time. It is often useful, because many commonly encountered forces are conservative.
Beyond Newton's Laws
Classical mechanics also includes descriptions of the complex motions of extended non-pointlike objects. The concepts of angular momentum rely on the same calculus used to describe one-dimensional motion.
There are two important alternative formulations of classical mechanics: Lagrangian mechanics and Hamiltonian mechanics. These, and other modern formulations, usually bypass the concept of "force", instead referring to other physical quantities, such as energy, for describing mechanical systems.
[edit] Classical transformations
Consider two reference frames S and S' . For observers in each of the reference frames an event has space-time coordinates of (x,y,z,t) in frame S and (x' ,y' ,z' ,t' ) in frame S' . Assuming time is measured the same in all reference frames, and if we require x = x' when t = 0, then the relation between the space-time coordinates of the same event observed from the reference frames S' and S, which are moving at a relative velocity of u in the x direction is:
- x' = x - ut
- y' = y
- z' = z
- t' = t
This set of formulas defines a group transformation known as the Galilean transformation (informally, the Galilean transform). This group is a limiting case of the Poincaré group used in special relativity. The limiting case applies when the velocity u is very small compared to c, the speed of light.
For some problems, it is convenient to use rotating coordinates (reference frames). Thereby one can either keep a mapping to a convenient inertial frame, or introduce additionally a fictitious centrifugal force and Coriolis force.
History
- See also: Timeline of classical mechanics
Some Greek philosophers of antiquity, among them Aristotle, may have been the first to maintain the idea that "everything happens for a reason" and that theoretical principles can assist in the understanding of nature. While, to a modern reader, many of these preserved ideas come forth as eminently reasonable, there is a conspicuous lack of both mathematical theory and controlled experiment, as we know it. These both turned out to be decisive factors in forming modern science, and they started out with classical mechanics.
An early experimental scientific method was introduced into mechanics in the 11th century by al-Biruni, who along with al-Khazini in the 12th century, unified statics and dynamics into the science of mechanics, and combined the fields of hydrostatics with dynamics to create the field of hydrodynamics.[2] Concepts related to Newton's laws of motion were also enunciated by several other Muslim physicists during the Middle Ages. Early versions of the law of inertia, known as Newton's first law of motion, and the concept relating to momentum, part of Newton's second law of motion, were described by Ibn al-Haytham (Alhacen)[3][4] and Avicenna.[5][6] The proportionality between force and acceleration, an important principle in classical mechanics, was first stated by Hibat Allah Abu'l-Barakat al-Baghdaadi,[7] and theories on gravity were developed by Ja'far Muhammad ibn Mūsā ibn Shākir,[8] Ibn al-Haytham,[9] and al-Khazini.[10] It is known that Galileo Galilei's mathematical treatment of acceleration and his concept of impetus[11] grew out of earlier medieval analyses of motion, especially those of Avicenna,[5] Ibn Bajjah,[12] and Jean Buridan.
The first published causal explanation of the motions of planets was Johannes Kepler's Astronomia nova published in 1609. He concluded, based on Tycho Brahe's observations of the orbit of Mars, that the orbits were ellipses. This break with ancient thought was happening around the same time that Galilei was proposing abstract mathematical laws for the motion of objects. He may (or may not) have performed the famous experiment of dropping two cannon balls of different masses from the tower of Pisa, showing that they both hit the ground at the same time. The reality of this experiment is disputed, but, more importantly, he did carry out quantitative experiments by rolling balls on an inclined plane. His theory of accelerated motion derived from the results of such experiments, and forms a cornerstone of classical mechanics.
As foundation for his principles of natural philosophy, Newton proposed three laws of motion, the law of inertia, his second law of acceleration, mentioned above, and the law of action and reaction, and hence laying the foundations for classical mechanics. Both Newtons second and third laws were given proper scientific and mathematical treatment in Newton's Philosophiæ Naturalis Principia Mathematica, which distinguishes them from earlier attempts at explaining similar phenomena, which were either incomplete, incorrect, or given little accurate mathematical expression. Newton also enunciated the principles of conservation of momentum and angular momentum. In Mechanics, Newton was also the first to provide the first correct scientific and mathematical formulation of gravity in Newton's law of universal gravitation. The combination of Newton's laws of motion and gravitation provide the fullest and most accurate description of classical mechanics. He demonstrated that these laws apply to everyday objects as well as to celestial objects. In particular, he obtained a theoretical explanation of Kepler's laws of motion of the planets.
Newton previously invented the calculus, of mathematics, and used it to perform the mathematical calculations. For acceptability, his book, the Principia, was formulated entirely in terms of the long established geometric methods, which were soon to be eclipsed by his calculus. However it was Leibniz who developed the notation of the derivative and integral preferred today.
Newton, and most of his contemporaries, with the notable exception of Huygens, worked on the assumption that classical mechanics would be able to explain all phenomena, including light, in the form of geometric optics. Even when discovering the so-called Newton's rings (a wave interference phenomenon) his explanation remained with his own corpuscular theory of light.
After Newton, classical mechanics became a principal field of study in mathematics as well as physics.
Some difficulties were discovered in the late 19th century that could only be resolved by more modern physics. Some of these difficulties related to compatibility with electromagnetic theory, and the famous Michelson-Morley experiment. The resolution of these problems led to the special theory of relativity, often included in the term classical mechanics.
A second set of difficulties related to thermodynamics. When combined with thermodynamics, classical mechanics leads to the Gibbs paradox of classical statistical mechanics, in which entropy is not a well-defined quantity. Black-body radiation was not explained without the introduction of quanta. As experiments reached the atomic level, classical mechanics failed to explain, even approximately, such basic things as the energy levels and sizes of atoms and the photo-electric effect. The effort at resolving these problems led to the development of quantum mechanics.
Since the end of the 20th century, the place of classical mechanics in physics has been no longer that of an independent theory. Emphasis has shifted to understanding the fundamental forces of nature as in the Standard model and its more modern extensions into a unified theory of everything.[13] Classical mechanics is a theory for the study of the motion of non-quantum mechanical, low-energy particles in weak gravitational fields.
Limits of validity
Many branches of classical mechanics are simplifications or approximations of more accurate forms; two of the most accurate being general relativity and relativistic statistical mechanics. Geometric optics is an approximation to the quantum theory of light, and does not have a superior "classical" form.
The Newtonian approximation to special relativity
Newtonian, or non-relativistic classical momentum
is the result of the first order Taylor approximation of the relativistic expression:
 , where
, where 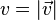
when expanded about
so it is only valid when the velocity is much less than the speed of light. Quantitatively speaking, the approximation is good so long as
For example, the relativistic cyclotron frequency of a cyclotron, gyrotron, or high voltage magnetron is given by  , where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest) mass m0 circling in a magnetic field. The (rest) mass of an electron is 511 keV. So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV. direct current accelerating voltage.
, where fc is the classical frequency of an electron (or other charged particle) with kinetic energy T and (rest) mass m0 circling in a magnetic field. The (rest) mass of an electron is 511 keV. So the frequency correction is 1% for a magnetic vacuum tube with a 5.11 kV. direct current accelerating voltage.
The classical approximation to quantum mechanics
The ray approximation of classical mechanics breaks down when the de Broglie wavelength is not much smaller than other dimensions of the system. For non-relativistic particles, this wavelength is
where h is Planck's constant and p is the momentum.
Again, this happens with electrons before it happens with heavier particles. For example, the electrons used by Clinton Davisson and Lester Germer in 1927, accelerated by 54 volts, had a wave length of 0.167 nm, which was long enough to exhibit a single diffraction side lobe when reflecting from the face of a nickel crystal with atomic spacing of 0.215 nm. With a larger vacuum chamber, it would seem relatively easy to increase the angular resolution from around a radian to a milliradian and see quantum diffraction from the periodic patterns of integrated circuit computer memory.
More practical examples of the failure of classical mechanics on an engineering scale are conduction by quantum tunneling in tunnel diodes and very narrow transistor gates in integrated circuits.
Classical mechanics is the same extreme high frequency approximation as geometric optics. It is more often accurate because it describes particles and bodies with rest mass. These have more momentum and therefore shorter De Broglie wavelengths than massless particles, such as light, with the same kinetic energies.
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference which belongs to a set of frames in which physical laws hold in the same and simplest form. According to the first postulate of special relativity, all physical laws take their simplest form in an inertial frame, and there exist multiple inertial frames interrelated by uniform translation: [1]
Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.
– Albert Einstein: The foundation of the general theory of relativity, Section A, §1
The principle of simplicity can be used within Newtonian physics as well as in special relativity; see Nagel[2] and also Blagojević.[3]
The laws of Newtonian mechanics do not always hold in their simplest form...If, for instance, an observer is placed on a disc rotating relative to the earth, he/she will sense a 'force' pushing him/her toward the periphery of the disc, which is not caused by any interaction with other bodies. Here, the acceleration is not the consequence of the usual force, but of the so-called inertial force. Newton's laws hold in their simplest form only in a family of reference frames, called inertial frames. This fact represents the essence of the Galilean principle of relativity:
The laws of mechanics have the same form in all inertial frames.– Milutin Blagojević: Gravitation and Gauge Symmetries, p. 4
In practical terms, the equivalence of inertial reference frames means that scientists within a box moving uniformly cannot determine their absolute velocity by any experiment (otherwise the differences would set up an absolute standard reference frame).[4][5] According to this definition, supplemented with the constancy of the speed of light, inertial frames of reference transform among themselves according to the Poincaré group of symmetry transformations, of which the Lorentz transformations are a subgroup.[6]
The expression inertial frame of reference (German: Inertialsystem) was coined by Ludwig Lange in 1885, to replace Newton's definitions of "absolute space and time" by a more operational definition.[7][8] As referenced by Iro, Lange proposed:[9]
A reference frame in which a mass point thrown from the same point in three different (non co-planar) directions follows rectilinear paths each time it is thrown, is called an inertial frame.
– L. Lange (1885) as quoted by Max von Laue in his book (1921) Die Relativitätstheorie, p. 34, and translated by Iro
A discussion of Lange's proposal can be found in Mach.[10]
The inadequacy of the notion of "absolute space" in Newtonian mechanics is spelled out by Blagojević:[11]
*The existence of absolute space contradicts the internal logic of classical mechanics since, according to Galilean principle of relativity, none of the inertial frames can be singled out.
*Absolute space does not explain inertial forces since they are related to acceleration with respect to any one of the inertial frames.
*Absolute space acts on physical objects by inducing their resistance to acceleration but it cannot be acted upon.– Milutin Blagojević: Gravitation and Gauage Symmetries, p. 5
The utility of operational definitions was carried much further in the special theory of relativity.[12] Some historical background including Lange's definition is provided by DiSalle, who says in summary: [13]
The original question, “relative to what frame of reference do the laws of motion hold?” is revealed to be wrongly posed. For the laws of motion essentially determine a class of reference frames, and (in principle) a procedure for constructing them.
Contents |
Newton's inertial frame of reference

 . Frame S' has an arbitrary but fixed rotation with respect to frame S. They are both inertial frames provided a body not subject to forces appears to move in a straight line. If that motion is seen in one frame, it will also appear that way in the other.
. Frame S' has an arbitrary but fixed rotation with respect to frame S. They are both inertial frames provided a body not subject to forces appears to move in a straight line. If that motion is seen in one frame, it will also appear that way in the other.Within the realm of Newtonian mechanics, an inertial frame of reference, or inertial reference frame, is one in which Newton's first law of motion is valid.[14] However, the principle of special relativity generalizes the notion of inertial frame to include all physical laws, not simply Newton's first law.
Newton viewed the first law as valid in any reference frame moving with uniform velocity relative to the fixed stars;[15] that is, neither rotating nor accelerating relative to the stars.[16] Today the notion of "absolute space" is abandoned, and an inertial frame in the field of classical mechanics is defined as:[17][18]
An inertial frame of reference is one in which the motion of a particle not subject to forces is in a straight line at constant speed.
Hence, with respect to an inertial frame, an object or body accelerates only when a physical force is applied, and (following Newton's first law of motion), in the absence of a net force, a body at rest will remain at rest and a body in motion will continue to move uniformly—that is, in a straight line and at constant speed. Newtonian inertial frames transform among each other according to the Galilean group of symmetries.
If this rule is interpreted as saying that straight-line motion is an indication of zero net force, the rule does not identify inertial reference frames, because straight-line motion can be observed in a variety of frames. If the rule is interpreted as defining an inertial frame, then we have to be able to determine when zero net force is applied. The problem was summarized by Einstein:[19]
The weakness of the principle of inertia lies in this, that it involves an argument in a circle: a mass moves without acceleration if it is sufficiently far from other bodies; we know that it is sufficiently far from other bodies only by the fact that it moves without acceleration.
– Albert Einstein: The Meaning of Relativity, p. 58
There are several approaches to this issue. One approach is to argue that all real forces drop off with distance from their sources in a known manner, so we have only to be sure that we are far enough away from all sources to insure that no force is present.[20] A possible issue with this approach is the historically long-lived view that the distant universe might affect matters (Mach's principle). Another approach is to identify all real sources for real forces and account for them. A possible issue with this approach is that we might miss something, or account inappropriately for their influence (Mach's principle again?). A third approach is to look at the way the forces transform when we shift reference frames. Fictitious forces, those that arise due to the acceleration of a frame, disappear in inertial frames, and have complicated rules of transformation in general cases. On the basis of universality of physical law and the request for frames where the laws are most simply expressed, inertial frames are distinguished by the absence of such fictitious forces.
Newton enunciated a principle of relativity himself in one of his corollaries to the laws of motion:[21][22]
The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forward in a straight line.
– Isaac Newton: Principia, Corollary V, p. 88 in Andrew Motte translation
This principle differs from the special principle in two ways: first, it is restricted to mechanics, and second, it makes no mention of simplicity. It shares with the special principle the invariance of the form of the description among mutually translating reference frames.[23] The role of fictitious forces in classifying reference frames is pursued further below.
Non-inertial reference frames
- See also: Non-inertial frame and Rotating spheres
Inertial and non-inertial reference frames can be distinguished by the absence or presence of fictitious forces, as explained shortly.[24][25]
The effect of his being in the noninertial frame is to require the observer to introduce a fictitious force into his calculations….
– Sidney Borowitz and Lawrence A Bornstein in A Contemporary View of Elementary Physics, p. 138
The presence of fictitious forces indicates the physical laws are not the simplest laws available so, in terms of the special principle of relativity, a frame where fictitious forces are present is not an inertial frame:[26]
The equations of motion in an non-inertial system differ from the equations in an inertial system by additional terms called inertial forces. This allows us to detect experimentally the non-inertial nature of a system.
– V. I. Arnol'd: Mathematical Methods of Classical Mechanics Second Edition, p. 129
Bodies in non-inertial reference frames are subject to so-called fictitious forces (pseudo-forces); that is, forces that result from the acceleration of the reference frame itself and not from any physical force acting on the body. Examples of fictitious forces are the centrifugal force and the Coriolis force in rotating reference frames.
How then, are "fictitious' forces to be separated from "real" forces? It is hard to apply the Newtonian definition of an inertial frame without this separation. For example, consider a stationary object in an inertial frame. Being at rest, no net force is applied. But in a frame rotating about a fixed axis, the object appears to move in a circle, and is subject to centripetal force (which is made up of the Coriolis force and the centrifugal force). How can we decide that the rotating frame is a non-inertial frame? There are two approaches to this resolution: one approach is to look for the origin of the fictitious forces (the Coriolis force and the centrifugal force). We will find there are no sources for these forces, no originating bodies.[27] A second approach is to look at a variety of frames of reference. For any inertial frame, the Coriolis force and the centrifugal force disappear, so application of the principle of special relativity would identify these frames where the forces disappear as sharing the same and the simplest physical laws, and hence rule that the rotating frame is not an inertial frame.
Newton examined this problem himself using rotating spheres, as shown in Figure 2 and Figure 3. He pointed out that if the spheres are not rotating, the tension in the tying string is measured as zero in every frame of reference.[28] If the spheres only appear to rotate (that is, we are watching stationary spheres from a rotating frame), the zero tension in the string is accounted for by observing that the centripetal force is supplied by the centrifugal and Coriolis forces in combination, so no tension is needed. If the spheres really are rotating, the tension observed is exactly the centripetal force required by the circular motion. Thus, measurement of the tension in the string identifies the inertial frame: it is the one where the tension in the string provides exactly the centripetal force demanded by the motion as it is observed in that frame, and not a different value. That is, the inertial frame is the one where the fictitious forces vanish. (See Rotating spheres for original text and mathematical formulation.)
So much for fictitious forces due to rotation. However, for linear acceleration, Newton expressed the idea of undetectability of straight-line accelerations held in common:[22]
If bodies, any how moved among themselves, are urged in the direction of parallel lines by equal accelerative forces, they will continue to move among themselves, after the same manner as if they had been urged by no such forces.
– Isaac Newton: Principia Corollary VI, p. 89, in Andrew Motte translation
This principle generalizes the notion of an inertial frame. For example, an observer confined in a free-falling lift will assert that he himself is a valid inertial frame, even if he is accelerating under gravity, so long as he has no knowledge about anything outside the lift. So, strictly speaking, inertial frame is a relative concept. With this in mind, we can define inertial frames collectively as a set of frames which are stationary or moving at constant velocity with respect to each other, so that a single inertial frame is defined as an element of this set.
For these ideas to apply, everything observed in the frame has to be subject to a base-line, common acceleration shared by the frame itself. That situation would apply, for example, to the elevator example, where all objects are subject to the same gravitational acceleration, and the elevator itself accelerates at the same rate.
Newtonian mechanics
Classical mechanics, which includes relativity, assumes the equivalence of all inertial reference frames. Newtonian mechanics makes the additional assumptions of absolute space and absolute time. Given these two assumptions, the coordinates of the same event (a point in space and time) described in two inertial reference frames are related by a Galilean transformation
where  and t0 represent shifts in the origin of space and time, and
and t0 represent shifts in the origin of space and time, and  is the relative velocity of the two inertial reference frames. Under Galilean transformations, the time between two events (t2 − t1) is the same for all inertial reference frames and the distance between two simultaneous events (or, equivalently, the length of any object,
is the relative velocity of the two inertial reference frames. Under Galilean transformations, the time between two events (t2 − t1) is the same for all inertial reference frames and the distance between two simultaneous events (or, equivalently, the length of any object,  ) is also the same.
) is also the same.
Special relativity
Special relativity (SR) (also known as the special theory of relativity or STR) is the physical theory of measurement in inertial frames of reference proposed in 1905 by Albert Einstein (after the considerable and independent contributions of Hendrik Lorentz and Henri Poincaré and others) in the paper "On the Electrodynamics of Moving Bodies".[1] It generalizes Galileo's principle of relativity – that all uniform motion is relative, and that there is no absolute and well-defined state of rest (no privileged reference frames) – from mechanics to all the laws of physics, including both the laws of mechanics and of electrodynamics, whatever they may be.[2] Special relativity incorporates the principle that the speed of light is the same for all inertial observers regardless of the state of motion of the source.[3]
This theory has a wide range of consequences which have been experimentally verified, [4] including counter-intuitive ones such as length contraction, time dilation and relativity of simultaneity, contradicting the classical notion that the duration of the time interval between two events is equal for all observers. (On the other hand, it introduces the space-time interval, which is invariant.) Combined with other laws of physics, the two postulates of special relativity predict the equivalence of matter and energy, as expressed in the mass-energy equivalence formula E = mc2, where c is the speed of light in a vacuum.[5][6] The predictions of special relativity agree well with Newtonian mechanics in their common realm of applicability, specifically in experiments in which all velocities are small compared to the speed of light.
The theory is termed "special" because it applies the principle of relativity only to inertial frames. Einstein developed general relativity to apply the principle more generally, that is, to any frame, including accelerating frames, and that theory includes the effects of gravity.
Special relativity reveals that c is not just the velocity of a certain phenomenon, namely the propagation of electromagnetic radiation (light)—but rather a fundamental feature of the way space and time are unified as spacetime. A consequence of this is that it is impossible for any particle that has mass to be accelerated to the speed of light.
Postulates
In his autobiographical notes published in November 1949 Einstein described how he had arrived at the two fundamental postulates on which he based the special theory of relativity. After describing in detail the state of both mechanics and electrodynamics at the beginning of the 20th century, he wrote
"Reflections of this type made it clear to me as long ago as shortly after 1900, i.e., shortly after Planck's trailblazing work, that neither mechanics nor electrodynamics could (except in limiting cases) claim exact validity. Gradually I despaired of the possibility of discovering the true laws by means of constructive efforts based on known facts. The longer and the more desperately I tried, the more I came to the conviction that only the discovery of a universal formal principle could lead us to assured results... How, then, could such a universal principle be found?"[7]
He discerned two fundamental propositions that seemed to be the most assured, regardless of the exact validity of either the (then) known laws of mechanics or electrodynamics. These propositions were:(1) the constancy of the velocity of light, and (2) the independence of physical laws (especially the constancy of the velocity of light) from the choice of inertial system. In his initial presentation of special relativity in 1905 he expressed these postulates as:[8]
- The Principle of Relativity - The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems in uniform translatory motion relative to each other.
- The Principle of Invariant Light Speed - Light in vacuum propagates with the speed c (a fixed constant) in terms of any system of inertial coordinates, regardless of the state of motion of the light source.
It should be noted that the derivation of special relativity depends not only on these two explicit postulates, but also on several tacit assumptions (which are made in almost all theories of physics), including the isotropy and homogeneity of space and the independence of measuring rods and clocks from their past history.[9]
Following Einstein's original presentation of special relativity in 1905, many different sets of postulates have been proposed in various alternative derivations.[10] However, the most common set of postulates remains those employed by Einstein in his original paper. A more mathematical statement of the Principle of Relativity made later by Einstein, which introduces the concept of simplicity not mentioned above is:[11]
Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K' moving in uniform translation relatively to K.
– Albert Einstein: The foundation of the general theory of relativity, Section A, §1
The two postulates of special relativity imply the applicability to physical laws of the Poincaré group of symmetry transformations, of which the Lorentz transformations are a subset, thereby providing a mathematical framework for special relativity. Many of Einstein's papers present derivations of the Lorentz transformation based upon these two principles.[12]
Einstein consistently based the derivation of Lorentz invariance (the essential core of special relativity) on just the two basic principles of relativity and light-speed invariance. He wrote:
"The insight fundamental for the special theory of relativity is this: The assumptions relativity and light speed invariance are compatible if relations of a new type ("Lorentz transformation") are postulated for the conversion of coordinates and times of events... The universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen inertial system). This is a restricting principle for natural laws..."[7]
Thus many modern treatments of special relativity base it on the single postulate of universal Lorentz covariance, or, equivalently, on the single postulate of Minkowski spacetime.[13][14]
Mass-energy equivalence
- See also: Mass in special relativity
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy (the famous formula E = m c2).
Mass-energy equivalence does not follow from the two basic postulates of special relativity by themselves.[15] The first of Einstein's papers on this subject was Does the Inertia of a Body Depend upon its Energy Content? in 1905.[16] In this first paper and in each of his subsequent three papers on this subject,[17] Einstein augmented the two fundamental principles by postulating the relations involving momentum and energy of electromagnetic waves implied by Maxwell's equations (the assumption of which, of course, entails among other things the assumption of the constancy of the speed of light). It has been suggested that Einstein's original argument was fallacious.[18] Other authors suggest that the argument was merely inconclusive by virtue of some implicit assumptions lacking experimental verification at the time. [19]
Einstein acknowledged in his 1907 survey paper on special relativity that it was problematic to rely on Maxwell's equations for the heuristic mass-energy argument.[20] [21]
Lack of an absolute reference frame
The principle of relativity, which states that there is no preferred inertial reference frame, dates back to Galileo, and was incorporated into Newtonian Physics. However, in the late 19th century, the existence of electromagnetic waves led physicists to suggest that the universe was filled with a substance known as "aether", which would act as the medium through which these waves, or vibrations traveled. The aether was thought to constitute an absolute reference frame against which speeds could be measured. In other words, the aether was the only fixed or motionless thing in the universe. Aether supposedly had some wonderful properties: it was sufficiently elastic that it could support electromagnetic waves, and those waves could interact with matter, yet it offered no resistance to bodies passing through it. The results of various experiments, including the Michelson-Morley experiment, indicated that the Earth was always 'stationary' relative to the aether – something that was difficult to explain, since the Earth is in orbit around the Sun. Einstein's elegant solution was to discard the notion of an aether and an absolute state of rest. Special relativity is formulated so as to not assume that any particular frame of reference is special; rather, in relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in a vacuum is always measured to be c, even when measured by multiple systems that are moving at different (but constant) velocities.
Consequences
Einstein has said that all of the consequences of special relativity can be derived from examination of the Lorentz transformations.
These transformations, and hence special relativity, lead to different physical predictions than Newtonian mechanics when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything humans encounter that some of the effects predicted by relativity are initially counter-intuitive:
- Time dilation – the time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames (e.g., the twin paradox which concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that his or her twin sibling has aged much more).
- Relativity of simultaneity – two events happening in two different locations that occur simultaneously to one observer, may occur at different times to another observer (lack of absolute simultaneity).
- Lorentz contraction – the dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage).
- Composition of velocities – velocities (and speeds) do not simply 'add', for example if a rocket is moving at ⅔ the speed of light relative to an observer, and the rocket fires a missile at ⅔ of the speed of light relative to the rocket, the missile does not exceed the speed of light relative to the observer. (In this example, the observer would see the missile travel with a speed of 12/13 the speed of light.)
- Inertia and momentum – as an object's speed approaches the speed of light from an observer's point of view, its mass appears to increase thereby making it more and more difficult to accelerate it from within the observer's frame of reference.
- Equivalence of mass and energy, E = mc2 – The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that in any reaction a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
Reference frames, coordinates and the Lorentz transformation
- Full article: Lorentz transformations

Relativity theory depends on "reference frames". A reference frame is an observational perspective in space at rest, or in uniform motion, from which a position can be measured along 3 spatial axes. In addition, a reference frame has the ability to determine measurements of the time of events using a 'clock' (any reference device with uniform periodicity).
An event is an occurrence that can be assigned a single unique time and location in space relative to a reference frame: it is a "point" in space-time. Since the speed of light is constant in relativity in each and every reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four space-time coordinates: The time of occurrence and its 3-dimensional spatial location define a reference point. Let's call this reference frame S.
In relativity theory we often want to calculate the position of a point from a different reference point.
Suppose we have a second reference frame S', whose spatial axes and clock exactly coincide with that of S at time zero, but it is moving at a constant velocity  with respect to S along the
with respect to S along the  -axis.
-axis.
Since there is no absolute reference frame in relativity theory, a concept of 'moving' doesn't strictly exist, as everything is always moving with respect to some other reference frame. Instead, any two frames that move at the same speed in the same direction are said to be comoving. Therefore S and S' are not comoving.
Let's define the event to have space-time coordinates  in system S and
in system S and  in S'. Then the Lorentz transformation specifies that these coordinates are related in the following way:
in S'. Then the Lorentz transformation specifies that these coordinates are related in the following way:
where 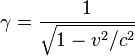 is called the Lorentz factor and
is called the Lorentz factor and  is the speed of light in a vacuum.
is the speed of light in a vacuum.
The  and
and 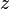 coordinates are unaffected, but the
coordinates are unaffected, but the  and
and 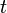 axes are mixed up by the transformation. In a way this transformation can be understood as a hyperbolic rotation.
axes are mixed up by the transformation. In a way this transformation can be understood as a hyperbolic rotation.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
Simultaneity
From the first equation of the Lorentz transformation in terms of coordinate differences
it is clear that two events that are simultaneous in frame S (satisfying 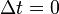 ), are not necessarily simultaneous in another inertial frame S' (satisfying
), are not necessarily simultaneous in another inertial frame S' (satisfying  ). Only if these events are colocal in frame S (satisfying
). Only if these events are colocal in frame S (satisfying  ), will they be simultaneous in another frame S'.
), will they be simultaneous in another frame S'.
Time dilation and length contraction
Writing the Lorentz transformation and its inverse in terms of coordinate differences we get
and
Suppose we have a clock at rest in the unprimed system S. Two consecutive ticks of this clock are then characterized by Δx = 0. If we want to know the relation between the times between these ticks as measured in both systems, we can use the first equation and find:
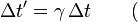 for events satisfying
for events satisfying 
This shows that the time Δt' between the two ticks as seen in the 'moving' frame S' is larger than the time Δt between these ticks as measured in the rest frame of the clock. This phenomenon is called time dilation.
Similarly, suppose we have a measuring rod at rest in the unprimed system. In this system, the length of this rod is written as Δx. If we want to find the length of this rod as measured in the 'moving' system S', we must make sure to measure the distances x' to the end points of the rod simultaneously in the primed frame S'. In other words, the measurement is characterized by Δt' = 0, which we can combine with the fourth equation to find the relation between the lengths Δx and Δx':
 for events satisfying
for events satisfying 
This shows that the length Δx' of the rod as measured in the 'moving' frame S' is shorter than the length Δx in its own rest frame. This phenomenon is called length contraction or Lorentz contraction.
These effects are not merely appearances; they are explicitly related to our way of measuring time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals will be different in another coordinate system moving with respect to the first, unless the events are also simultaneous. Similarly, these effects also relate to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spacial distance from each other when seen from another moving coordinate system.
See also the twin paradox.
Causality and prohibition of motion faster than light
- See also: Causality
In diagram 2 the interval AB is 'time-like'; i.e., there is a frame of reference in which event A and event B occur at the same location in space, separated only by occurring at different times. If A precedes B in that frame, then A precedes B in all frames. It is hypothetically possible for matter (or information) to travel from A to B, so there can be a causal relationship (with A the cause and B the effect).
The interval AC in the diagram is 'space-like'; i.e., there is a frame of reference in which event A and event C occur simultaneously, separated only in space. However there are also frames in which A precedes C (as shown) and frames in which C precedes A. If it were possible for a cause-and-effect relationship to exist between events A and C, then paradoxes of causality would result. For example, if A was the cause, and C the effect, then there would be frames of reference in which the effect preceded the cause. Although this in itself won't give rise to a paradox, one can show[22][23] that faster than light signals can be sent back into one's own past. A causal paradox can then be constructed by sending the signal if and only if no signal was received previously.
Therefore, one of the consequences of special relativity is that (assuming causality is to be preserved), no information or material object can travel faster than light. On the other hand, the logical situation is not as clear in the case of general relativity, so it is an open question whether there is some fundamental principle that preserves causality (and therefore prevents motion faster than light) in general relativity.
Even without considerations of causality, there are other strong reasons why faster-than-light travel is forbidden by special relativity. For example, if a constant force is applied to an object for a limitless amount of time, then integrating F = dp/dt gives a momentum that grows without bound, but this is simply because p = mγv approaches infinity as v approaches c. To an observer who is not accelerating, it appears as though the object's inertia is increasing, so as to produce a smaller acceleration in response to the same force. This behavior is in fact observed in particle accelerators.
See also the Tachyonic Antitelephone.
[edit] Composition of velocities
If the observer in S sees an object moving along the x axis at velocity w, then the observer in the S' system, a frame of reference moving at velocity v in the x direction with respect to S, will see the object moving with velocity w' where
This equation can be derived from the space and time transformations above.
Notice that if the object were moving at the speed of light in the S system (i.e. w = c), then it would also be moving at the speed of light in the S' system. Also, if both w and v are small with respect to the speed of light, we will recover the intuitive Galilean transformation of velocities:  .
.
Relativistic mechanics
In addition to modifying notions of space and time, special relativity forces one to reconsider the concepts of mass, momentum, and energy, all of which are important constructs in Newtonian mechanics. Special relativity shows, in fact, that these concepts are all different aspects of the same physical quantity in much the same way that it shows space and time to be interrelated.
There are a couple of (equivalent) ways to define momentum and energy in SR. One method uses conservation laws. If these laws are to remain valid in SR they must be true in every possible reference frame. However, if one does some simple thought experiments using the Newtonian definitions of momentum and energy, one sees that these quantities are not conserved in SR. One can rescue the idea of conservation by making some small modifications to the definitions to account for relativistic velocities. It is these new definitions which are taken as the correct ones for momentum and energy in SR.
The energy and momentum of an object with invariant mass m (also called rest mass in the case of a single particle), moving with velocity v with respect to a given frame of reference, are given by
respectively, where γ (the Lorentz factor) is given by
The quantity γm is often called the relativistic mass of the object in the given frame of reference, [24] although recently this concept is falling in disuse, and Lev B. Okun suggested that "this terminology [...] has no rational justification today", and should no longer be taught. [25] Other physicists, including Wolfgang Rindler and T. R. Sandin, have argued that relativistic mass is a useful concept and there is little reason to stop using it. [26] See Mass in special relativity for more information on this debate. Some authors use the symbol m to refer to relativistic mass, and the symbol m0 to refer to rest mass. [27]
The energy and momentum of an object with invariant mass m are related by the formulas
The first is referred to as the relativistic energy-momentum equation. While the energy E and the momentum p depend on the frame of reference in which they are measured, the quantity E2 − (pc)2 is invariant, being equal to the squared invariant mass of the object (up to the multiplicative constant c4).
It should be noted that the invariant mass of a system
is greater than the sum of the rest masses of the particles it is composed of (unless they are all stationary with respect to the center of mass of the system, and hence to each other). The sum of rest masses is not even always conserved in closed systems, since rest mass may be converted to particles which individually have no mass, such as photons. Invariant mass, however, is conserved and invariant for all observers, so long as the system remains closed. This is due to the fact that even massless particles contribute invariant mass to systems, as also does the kinetic energy of particles. Thus, even under transformations of rest mass to photons or kinetic energy, the invariant mass of a system which contains these energies still reflects the invariant mass associated with them.
E=mc2
For massless particles, m is zero. The relativistic energy-momentum equation still holds, however, and by substituting m with 0, the relation E = pc is obtained. This is Einstein's equation for photons.
A particle which has no rest mass can nevertheless contribute to the total invariant mass of a system, since some or all of its momentum is canceled by another particle, causing a contribution to the system's invariant mass due to the photon's energy. For single photons this does not happen, since the energy and momentum terms exactly cancel.
Looking at the above formula for invariant mass of a system, one sees that, when a single massive object is at rest (v = 0, p = 0), there is a non-zero mass remaining: mrest = E / c2. The corresponding energy, which is also the total energy when a single particle is at rest, is referred to as "rest energy". In systems of particles which are seen from a moving inertial frame, total energy increases and so does momentum. However, for single particles the rest mass remains constant, and for systems of particles the invariant mass remain constant, because in both cases, the energy and momentum increases subtract from each other, and cancel. Thus, the invariant mass of systems of particles is a calculated constant for all observers, as is the rest mass of single particles.
For systems, the inertial frame in which the momenta of all particles sums to zero, is called the center of momentum frame. In this special frame, the relativistic energy-momentum equation has p = 0, and thus gives the mass of the system as merely the total energy of all parts of the system, divided by c2
This is the mass of any system which is measured in a frame where it has zero total momentum, such as a bottle of hot gas on a scale. In such a system, the mass which the scale weighs is the invariant mass, and it depends on the total energy of the system. It is thus more than the sum of the rest masses of the molecules, but also includes all the totaled energies in the system as well. Like energy and momentum, the invariant mass of closed systems cannot be changed so long as the system is closed, because the total relativistic energy of the system remains constant so long as nothing can enter or leave it.
An increase in the energy of such a system which is caused by translating the system to an inertial frame which is not the center of momentum frame, causes an increase in energy and momentum without an increase in invariant mass. Einstein's famous E = mc^2 equation, however, applies only to closed systems in their center-of-momentum frame where momentum sums to zero.
Taking this formula at face value, we see that in relativity, mass is simply another form of energy. In 1927 Einstein remarked about special relativity: Under this theory mass is not an unalterable magnitude, but a magnitude dependent on (and, indeed, identical with) the amount of energy.[28]
Einstein was not referring to closed systems in this remark, however. For, even in his 1905 paper, which first derived the relationship between mass and energy, Einstein showed that the energy of an object had to be increased for its invariant mass (rest mass) to increase. In such cases, the system is not closed (in Einstein's thought experiment, for example, a mass gives off two photons, which are lost).
In a closed system the total energy, the total momentum, and hence the total invariant mass are conserved. Einstein's formula for invariant mass translates to its simplest ΔE = mc^2 form, however, in non-closed systems in which energy is allowed to escape (for example, as heat and light). Einstein's equation shows that such systems must lose mass, in accordance with the above formula, in proportion to the energy they lose to the surroundings. Conversely, if one can measure the differences in mass between a system before it undergoes a reaction which releases heat and light, and the system after the reaction when heat and light have escaped, one can estimate the amount of energy which escapes the system. In both nuclear and chemical reactions, such energy represents the difference in binding energies of electrons in atoms (for chemistry) or between nucleons in nuclei (in atomic reactions). In both cases, the mass difference between reactants and (cooled) products measures the mass of heat and light which will escape the reaction, and thus (using the equation) give the equivalent energy of heat and light which may be emitted if the reaction proceeds.
In chemistry, the mass differences associated with the emitted energy are too small to measure. However, in nuclear reactions the energies are so large that they are associated with mass differences, which can be estimated in advance, if the products and reactants have been weighed (atoms can be weighed indirectly by using atomic masses, which are always the same for each nuclide). Thus, Einstein's formula becomes important when one has measured the masses of different atomic nuclei. By looking at the difference in masses, one can predict which nuclei have stored energy that can be released by certain nuclear reactions, providing important information which was useful in the development of nuclear energy and, consequently, the nuclear bomb. Historically, for example, Lise Meitner was able to use the mass differences in nuclei to estimate that there was enough energy available to make nuclear fission a favorable process. The implications of this formula on 20th-century life have made it one of the most famous equations in all of science.
Because the E = mc^2 equation applies to systems only in their center of momentum frame, it has been popularly misunderstood to mean that mass may be converted to energy, after which the mass disappears. This is incorrect, as mass never disappears in the center of momentum frame, since this type of mass is invariant mass, and is thus conserved unless it is allowed to escape. Instead, this equation, in context, means only that when any energy is added to, or escapes from, a system in the center-of-momentum frame, the system will be measured as having gained or lost mass, in proportion to the energy added or removed. Thus, in theory, if even an atomic bomb were placed in a box strong enough to hold its blast, and detonated upon a scale, the mass of this closed system would not change, and the scale would not move. Only when a transparent "window" was opened in the super-strong plasma-filled box, and light and heat were allowed to escape in a beam, and the bomb components to cool, would the system lose the mass associated with the energy of the blast. In a 21 kiloton bomb, for example, about a gram of light and heat is created. If this heat and light were allowed to escape, the remains of the bomb would lose a gram of mass, as it cooled. However, invariant mass cannot be destroyed in special relativity, but only moved from place to place. In this thought-experiment, the light and heat carry away the gram of mass, and would therefore deposit this gram of mass in the objects that absorb them.
Force
In special relativity, Newton's second law does not hold in its form F = ma, but it does if it is expressed as
where p is the momentum as defined above (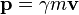 )and "m" is the invariant mass. Thus, the force is given by
)and "m" is the invariant mass. Thus, the force is given by
Carrying out the derivatives gives
which, taking into account the identity  , can also be expressed as
, can also be expressed as
If the acceleration is separated into the part parallel to the velocity and the part perpendicular to it, one gets
Consequently in some old texts, γm3 is referred to as the longitudinal mass, and γm is referred to as the transverse mass, which is the same as the relativistic mass.
For the four-force, see below.
Kinetic energy
The Work-energy Theorem says [29] the change in kinetic energy is equal to the work done on the body, that is
If in the initial state the body was at rest (γ0 = 1) and in the final state it has speed v (γ1 = γ), the kinetic energy is K = (γ − 1)mc2, a result that can be directly obtained by subtracting the rest energy mc2 from the total relativistic energy γmc2.
Application in cyclotrons
The application of the above in cyclotrons is immediate: [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40]
In the presence of a magnetic field only, the Lorentz force is:
Since:
it follows that:
meaning that γ is constant, and so is v. This is instrumental in solving the equation of motion for a charge particle of charge q in a magnetic field of induction B as follows:
On the other hand:
Thus:
Separating by components, we obtain:
The solutions are:
By integrating one more time with respect to t the differential equations above we obtain the equations of motion: a circle of radius 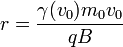 in the plane z=constant, where v0 is the initial speed of the particle entering the cyclotron. Notice that this calculation ignores the Abraham-Lorentz force which is the reaction to the emission of electromagnetic radiation by the particle. If the speed is held constant by applying an electric field, then the magnitude of the acceleration is constant,
in the plane z=constant, where v0 is the initial speed of the particle entering the cyclotron. Notice that this calculation ignores the Abraham-Lorentz force which is the reaction to the emission of electromagnetic radiation by the particle. If the speed is held constant by applying an electric field, then the magnitude of the acceleration is constant, 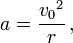 but its direction keeps changing in a cyclotron. The jerk is proportional with the second time derivative of speed:
but its direction keeps changing in a cyclotron. The jerk is proportional with the second time derivative of speed:
Because the jerk is directed opposite to the velocity, the Abraham-Lorentz force tends to slow the particle down. Note that the Abraham-Lorentz force is much smaller than the Lorentz force:
so, it can be ignored in most computations.
Classical limit
For velocities much smaller than that of light, γ can be expanded into a Taylor series, obtaining:
Neglecting the terms with c2 and higher in the denominator, these formulas agree with the standard definitions of Newtonian kinetic energy and momentum. This is as it should be, for special relativity must agree with Newtonian mechanics at low velocities.
The geometry of space-time
- See also: Spacetime
SR uses a 'flat' 4-dimensional Minkowski space, which is an example of a space-time. This space, however, is very similar to the standard 3 dimensional Euclidean space, and fortunately by that fact, very easy to work with.
The differential of distance (ds) in cartesian 3D space is defined as:
where (dx1,dx2,dx3) are the differentials of the three spatial dimensions. In the geometry of special relativity, a fourth dimension is added, derived from time, so that the equation for the differential of distance becomes:
If we wished to make the time coordinate look like the space coordinates, we could treat time as imaginary: x4 = ict . In this case the above equation becomes symmetric:
This suggests what is in fact a profound theoretical insight as it shows that special relativity is simply a rotational symmetry of our space-time, very similar to rotational symmetry of Euclidean space. Just as Euclidean space uses a Euclidean metric, so space-time uses a Minkowski metric. Basically, SR can be stated in terms of the invariance of space-time interval (between any two events) as seen from any inertial reference frame. All equations and effects of special relativity can be derived from this rotational symmetry (the Poincaré group) of Minkowski space-time. According to Misner (1971 §2.3), ultimately the deeper understanding of both special and general relativity will come from the study of the Minkowski metric (described below) rather than a "disguised" Euclidean metric using ict as the time coordinate.
If we reduce the spatial dimensions to 2, so that we can represent the physics in a 3-D space
We see that the null geodesics lie along a dual-cone:
defined by the equation
or
Which is the equation of a circle with r=c×dt. If we extend this to three spatial dimensions, the null geodesics are the 4-dimensional cone:
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old", we are looking down this line of sight: a null geodesic. We are looking at an event a distance  away and a time d/c in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
away and a time d/c in the past. For this reason the null dual cone is also known as the 'light cone'. (The point in the lower left of the picture below represents the star, the origin represents the observer, and the line represents the null geodesic "line of sight".)
The cone in the -t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
The geometry of Minkowski space can be depicted using Minkowski diagrams, which are also useful in understanding many of the thought-experiments in special relativity.
Physics in spacetime
Here, we see how to write the equations of special relativity in a manifestly Lorentz covariant form. The position of an event in spacetime is given by a contravariant four vector whose components are:
where x1 = x and x2 = y and x3 = z as usual. We define x0 = ct so that the time coordinate has the same dimension of distance as the other spatial dimensions; in accordance with the general principle that space and time are treated equally, so far as possible.[41][42][43] Superscripts are contravariant indices in this section rather than exponents except when they indicate a square. Subscripts are covariant indices which also range from zero to three as with the spacetime gradient of a field φ:
Metric and transformations of coordinates
Having recognised the four-dimensional nature of spacetime, we are driven to employ the Minkowski metric, η, given in components (valid in any inertial reference frame) as:
which is equal to its reciprocal, ηαβ, in those frames.
Then we recognize that coordinate transformations between inertial reference frames are given by the Lorentz transformation tensor Λ. For the special case of motion along the x-axis, we have:
which is simply the matrix of a boost (like a rotation) between the x and ct coordinates. Where μ' indicates the row and ν indicates the column. Also, β and γ are defined as:
More generally, a transformation from one inertial frame (ignoring translations for simplicity) to another must satisfy:
where there is an implied summation of  and
and  from 0 to 3 on the right-hand side in accordance with the Einstein summation convention. The Poincaré group is the most general group of transformations which preserves the Minkowski metric and this is the physical symmetry underlying special relativity.
from 0 to 3 on the right-hand side in accordance with the Einstein summation convention. The Poincaré group is the most general group of transformations which preserves the Minkowski metric and this is the physical symmetry underlying special relativity.
All proper physical quantities are given by tensors. So to transform from one frame to another, we use the well-known tensor transformation law
Where  is the reciprocal matrix of
is the reciprocal matrix of 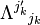 .
.
To see how this is useful, we transform the position of an event from an unprimed coordinate system S to a primed system S', we calculate
which is the Lorentz transformation given above. All tensors transform by the same rule.
The squared length of the differential of the position four-vector  constructed using
constructed using
is an invariant. Being invariant means that it takes the same value in all inertial frames, because it is a scalar (0 rank tensor), and so no Λ appears in its trivial transformation. Notice that when the line element  is negative that
is negative that  is the differential of proper time, while when
is the differential of proper time, while when  is positive,
is positive, 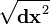 is differential of the proper distance.
is differential of the proper distance.
The primary value of expressing the equations of physics in a tensor form is that they are then manifestly invariant under the Poincaré group, so that we do not have to do a special and tedious calculation to check that fact. Also in constructing such equations we often find that equations previously thought to be unrelated are, in fact, closely connected being part of the same tensor equation.
Velocity and acceleration in 4D
Recognising other physical quantities as tensors also simplifies their transformation laws. First note that the velocity four-vector Uμ is given by
Recognising this, we can turn the awkward looking law about composition of velocities into a simple statement about transforming the velocity four-vector of one particle from one frame to another. Uμ also has an invariant form:
So all velocity four-vectors have a magnitude of c. This is an expression of the fact that there is no such thing as being at coordinate rest in relativity: at the least, you are always moving forward through time. The acceleration 4-vector is given by  . Given this, differentiating the above equation by τ produces
. Given this, differentiating the above equation by τ produces
So in relativity, the acceleration four-vector and the velocity four-vector are orthogonal.
Momentum in 4D
The momentum and energy combine into a covariant 4-vector:
where m is the invariant mass.
The invariant magnitude of the momentum 4-vector is:
We can work out what this invariant is by first arguing that, since it is a scalar, it doesn't matter which reference frame we calculate it, and then by transforming to a frame where the total momentum is zero.
We see that the rest energy is an independent invariant. A rest energy can be calculated even for particles and systems in motion, by translating to a frame in which momentum is zero.
The rest energy is related to the mass according to the celebrated equation discussed above:
Note that the mass of systems measured in their center of momentum frame (where total momentum is zero) is given by the total energy of the system in this frame. It may not be equal to the sum of individual system masses measured in other frames.
Force in 4D
To use Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the four-force. It is the rate of change of the above energy momentum four-vector with respect to proper time. The covariant version of the four-force is:
where  is the proper time.
is the proper time.
In the rest frame of the object, the time component of the four force is zero unless the "invariant mass" of the object is changing in which case it is the negative of that rate of change times c. In general, though, the components of the four force are not equal to the components of the three-force, because the three force is defined by the rate of change of momentum with respect to coordinate time, i.e.  while the four force is defined by the rate of change of momentum with respect to proper time, i.e.
while the four force is defined by the rate of change of momentum with respect to proper time, i.e.  .
.
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector. The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is −1/c times the power transferred to that cell divided by the volume of the cell. This will be used below in the section on electromagnetism.
Relativity and unifying electromagnetism
Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation-speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.
The Lorentz transformation of the electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic field. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Electromagnetism in 4D
Maxwell's equations in the 3D form are already consistent with the physical content of special relativity. But we must rewrite them to make them manifestly invariant.[44]
The charge density  and current density
and current density ![[J_x,J_y,J_z] \!](http://upload.wikimedia.org/math/b/b/d/bbda214f893097e844ca77ead238f3ea.png) are unified into the current-charge 4-vector:
are unified into the current-charge 4-vector:
The law of charge conservation,  , becomes:
, becomes:
The electric field ![[E_x,E_y,E_z] \!](http://upload.wikimedia.org/math/d/3/2/d32f98f806351056af76cc06b92c6675.png) and the magnetic induction
and the magnetic induction ![[B_x,B_y,B_z] \!](http://upload.wikimedia.org/math/4/b/0/4b079b6a4f51cb469344ef7055ab9ad5.png) are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
are now unified into the (rank 2 antisymmetric covariant) electromagnetic field tensor:
The density,  , of the Lorentz force,
, of the Lorentz force, 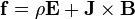 , exerted on matter by the electromagnetic field becomes:
, exerted on matter by the electromagnetic field becomes:
Faraday's law of induction, 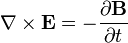 , and Gauss's law for magnetism,
, and Gauss's law for magnetism, 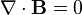 , combine to form:
, combine to form:
Although there appear to be 64 equations here, it actually reduces to just four independent equations. Using the antisymmetry of the electromagnetic field one can either reduce to an identity (0=0) or render redundant all the equations except for those with λ,μ,ν = either 1,2,3 or 2,3,0 or 3,0,1 or 0,1,2.
The electric displacement ![[D_x,D_y,D_z] \!](http://upload.wikimedia.org/math/c/3/e/c3e5dbe4aa735fb8c654c990852fdadf.png) and the magnetic field
and the magnetic field ![[H_x,H_y,H_z] \!](http://upload.wikimedia.org/math/e/4/a/e4a5c51917445501b7ac0e606c9bba14.png) are now unified into the (rank 2 antisymmetric contravariant) electromagnetic displacement tensor:
are now unified into the (rank 2 antisymmetric contravariant) electromagnetic displacement tensor:
Ampère's law,  , and Gauss's law,
, and Gauss's law, 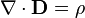 , combine to form:
, combine to form:
In a vacuum, the constitutive equations are:
Antisymmetry reduces these 16 equations to just six independent equations. Because it is usual to define 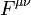 by
by
the constitutive equations may, in a vacuum, be combined with Ampère's law etc. to get:
The energy density of the electromagnetic field combines with Poynting vector and the Maxwell stress tensor to form the 4D electromagnetic stress-energy tensor. It is the flux (density) of the momentum 4-vector and as a rank 2 mixed tensor it is:
where 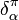 is the Kronecker delta. When upper index is lowered with η, it becomes symmetric and is part of the source of the gravitational field.
is the Kronecker delta. When upper index is lowered with η, it becomes symmetric and is part of the source of the gravitational field.
The conservation of linear momentum and energy by the electromagnetic field is expressed by:
where 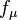 is again the density of the Lorentz force. This equation can be deduced from the equations above (with considerable effort).
is again the density of the Lorentz force. This equation can be deduced from the equations above (with considerable effort).
Status
Special relativity is accurate only when gravitational potential is much less than c2; in a strong gravitational field one must use general relativity (which becomes special relativity at the limit of weak field). At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravity. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10-20)[45] and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.
Because of the freedom one has to select how one defines units of length and time in physics, it is possible to make one of the two postulates of relativity a tautological consequence of the definitions, but one cannot do this for both postulates simultaneously, as when combined they have consequences which are independent of one's choice of definition of length and time. See Taiji relativity.
Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) - thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See Status of special relativity for a more detailed discussion.
A few key experiments can be mentioned that led to special relativity:
- The Trouton–Noble experiment showed that the torque on a capacitor is independent on position and inertial reference frame – such experiments led to the first postulate
- The famous Michelson-Morley experiment gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
A number of experiments have been conducted to test special relativity against rival theories. These include:
- Kaufmann-Bucherer-Neumann experiments – electron deflection in approximate agreement with Lorentz-Einstein prediction.
- Fizeau experiment - speed of light in moving media in accordance with relativistic velocity addition
- Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Rossi-Hall experiment – relativistic effects on a fast-moving particle's half-life
- Experiments to test emitter theory demonstrated that the speed of light is independent of the speed of the emitter.
- Hammar experiment – no "aether flow obstruction"
In addition, particle accelerators routinely accelerate and measure the properties of particles moving at near the speed of light, where their behavior is completely consistent with relativity theory and inconsistent with the earlier Newtonian mechanics. These machines would simply not work if they were not engineered according to relativistic principles.
Modern Physics
Quantum mechanics
| Quantum mechanics | ||||||||
 | ||||||||
| Uncertainty principle
| ||||||||
| Introduction to...
Mathematical formulation of...
| ||||||||

Quantum mechanics is the study of mechanical systems whose dimensions are close to the atomic scale, such as molecules, atoms, electrons, protons and other subatomic particles. Quantum mechanics is a fundamental branch of physics with wide applications. Quantum theory generalizes classical mechanics to provide accurate descriptions for many previously unexplained phenomena such as black body radiation and stable electron orbits. The effects of quantum mechanics become evident at the atomic and subatomic level, and they are typically not observable on macroscopic scales. Superfluidity is one of the known exceptions to this rule.
Contents |
Overview
The word “Quantum” came from the Latin word which means "how great" or "how much." In quantum mechanics, it refers to a discrete unit that quantum theory assigns to certain physical quantities, such as the energy of an atom at rest (see Figure 1, at right). The discovery that waves have discrete energy packets (called quanta) that behave in a manner similar to particles led to the branch of physics that deals with atomic and subatomic systems which we today call quantum mechanics. It is the underlying mathematical framework of many fields of physics and chemistry, including condensed matter physics, solid-state physics, atomic physics, molecular physics, computational chemistry, quantum chemistry, particle physics, and nuclear physics. The foundations of quantum mechanics were established during the first half of the twentieth century by Werner Heisenberg, Max Planck, Louis de Broglie, Albert Einstein, Niels Bohr, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli and others. Some fundamental aspects of the theory are still actively studied.
Quantum mechanics is essential to understand the behavior of systems at atomic length scales and smaller. For example, if classical mechanics governed the workings of an atom, electrons would rapidly travel towards and collide with the nucleus, making stable atoms impossible. However, in the natural world the electrons normally remain in an unknown orbital path around the nucleus, defying classical electromagnetism.
Quantum mechanics was initially developed to provide a better explanation of the atom, especially the spectra of light emitted by different atomic species. The quantum theory of the atom was developed as an explanation for the electron's staying in its orbital, which could not be explained by Newton's laws of motion and by Maxwell's laws of classical electromagnetism.
In the formalism of quantum mechanics, the state of a system at a given time is described by a complex wave function (sometimes referred to as orbitals in the case of atomic electrons), and more generally, elements of a complex vector space. This abstract mathematical object allows for the calculation of probabilities of outcomes of concrete experiments. For example, it allows one to compute the probability of finding an electron in a particular region around the nucleus at a particular time. Contrary to classical mechanics, one can never make simultaneous predictions of conjugate variables, such as position and momentum, with arbitrary accuracy. For instance, electrons may be considered to be located somewhere within a region of space, but with their exact positions being unknown. Contours of constant probability, often referred to as “clouds” may be drawn around the nucleus of an atom to conceptualize where the electron might be located with the most probability. Heisenberg's uncertainty principle quantifies the inability to precisely locate the particle.
The other exemplar that led to quantum mechanics was the study of electromagnetic waves such as light. When it was found in 1900 by Max Planck that the energy of waves could be described as consisting of small packets or quanta, Albert Einstein exploited this idea to show that an electromagnetic wave such as light could be described by a particle called the photon with a discrete energy dependent on its frequency. This led to a theory of unity between subatomic particles and electromagnetic waves called wave–particle duality in which particles and waves were neither one nor the other, but had certain properties of both. While quantum mechanics describes the world of the very small, it also is needed to explain certain “macroscopic quantum systems” such as superconductors and superfluids.
Broadly speaking, quantum mechanics incorporates four classes of phenomena that classical physics cannot account for: (i) the quantization (discretization) of certain physical quantities, (ii) wave-particle duality, (iii) the uncertainty principle, and (iv) quantum entanglement. Each of these phenomena is described in detail in subsequent sections.
History
The history of quantum mechanics began essentially with the 1838 discovery of cathode rays by Michael Faraday, the 1859 statement of the black body radiation problem by Gustav Kirchhoff, the 1877 suggestion by Ludwig Boltzmann that the energy states of a physical system could be discrete, and the 1900 quantum hypothesis by Max Planck that any energy is radiated and absorbed in quantities divisible by discrete ‘energy elements’, E, such that each of these energy elements is proportional to the frequency ν with which they each individually radiate energy, as defined by the following formula:
where h is Planck's Action Constant. Although Planck insisted that this was simply an aspect of the absorption and radiation of energy and had nothing to do with the physical reality of the energy itself, in 1905, to explain the photoelectric effect (1839), i.e. that shining light on certain materials can function to eject electrons from the material, Albert Einstein postulated, as based on Planck’s quantum hypothesis, that light itself consists of individual quanta, which later came to be called photons (1926). From Einstein's simple postulation was borne a flurry of debating, theorizing and testing, and thus, the entire field of quantum physics.
Relativity and quantum mechanics
The modern world of physics is founded on two tested and demonstrably sound theories of general relativity and quantum mechanics —theories which appear to contradict one another. The defining postulates of both Einstein's theory of relativity and quantum theory are indisputably supported by rigorous and repeated empirical evidence. However, while they do not directly contradict each other theoretically (at least with regard to primary claims), they are resistant to being incorporated within one cohesive model.
Einstein himself is well known for rejecting some of the claims of quantum mechanics. While clearly inventive in this field, he did not accept the more philosophical consequences and interpretations of quantum mechanics, such as the lack of deterministic causality and the assertion that a single subatomic particle can occupy numerous areas of space at one time. He also was the first to notice some of the apparently exotic consequences of entanglement and used them to formulate the Einstein-Podolsky-Rosen paradox, in the hope of showing that quantum mechanics had unacceptable implications. This was 1935, but in 1964 it was shown by John Bell (see Bell inequality) that Einstein's assumption that quantum mechanics was correct, but had to be completed by hidden variables, was based on wrong philosophical assumptions. According to the paper of J. Bell and the Copenhagen interpretation (the common interpretation of quantum mechanics by physicists for decades), and contrary to Einstein's ideas, quantum mechanics was
- neither a "realistic" theory (since quantum measurements do not state pre-existing properties, but rather they prepare properties)
- nor a local theory (essentially not, because the state vector
 determines simultaneously the probability amplitudes at all sites,
determines simultaneously the probability amplitudes at all sites, 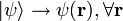 ).
).
The Einstein-Podolsky-Rosen paradox shows in any case that there exist experiments by which one can measure the state of one particle and instantaneously change the state of its entangled partner, although the two particles can be an arbitrary distance apart; however, this effect does not violate causality, since no transfer of information happens. These experiments are the basis of some of the most topical applications of the theory, quantum cryptography, which works well, although at small distances of typically  1000 km, being on the market since 2004.
1000 km, being on the market since 2004.
There do exist quantum theories which incorporate special relativity—for example, quantum electrodynamics (QED), which is currently the most accurately tested physical theory [1]—and these lie at the very heart of modern particle physics. Gravity is negligible in many areas of particle physics, so that unification between general relativity and quantum mechanics is not an urgent issue in those applications. However, the lack of a correct theory of quantum gravity is an important issue in cosmology.
Attempts at a unified theory
Inconsistencies arise when one tries to join the quantum laws with general relativity, a more elaborate description of spacetime which incorporates gravitation. Resolving these inconsistencies has been a major goal of twentieth- and twenty-first-century physics. Many prominent physicists, including Stephen Hawking, have labored in the attempt to discover a "Grand Unification Theory" that combines not only different models of subatomic physics, but also derives the universe's four forces—the strong force, electromagnetism, weak force, and gravity— from a single force or phenomenon.
Quantum mechanics and classical physics
Predictions of quantum mechanics have been verified experimentally to a very high degree of accuracy. Thus, the current logic of correspondence principle between classical and quantum mechanics is that all objects obey laws of quantum mechanics, and classical mechanics is just a quantum mechanics of large systems (or a statistical quantum mechanics of a large collection of particles). Laws of classical mechanics thus follow from laws of quantum mechanics at the limit of large systems or large quantum numbers.
Main differences between classical and quantum theories have already been mentioned above in the remarks on the Einstein-Podolsky-Rosen paradox. Essentially the difference boils down to the statement that quantum mechanics is coherent (addition of amplitudes), whereas classical theories are incoherent (addition of intensities). Thus, such quantities as coherence lengths and coherence times come into play. For microscopic bodies the extension of the system is certainly much smaller than the coherence length; for macroscopic bodies one expects that it should be the other way round.
This is in accordance with the following observations:
Many “macroscopic” properties of “classic” systems are direct consequences of quantum behavior of its parts. For example, stability of bulk matter (which consists of atoms and molecules which would quickly collapse under electric forces alone), rigidity of this matter, mechanical, thermal, chemical, optical and magnetic properties of this matter—they are all results of interaction of electric charges under the rules of quantum mechanics.
Whilst seemingly exotic behavior of matter posited by quantum mechanics and relativity theory become more apparent when dealing with extremely fast-moving or extremely tiny particles, the laws of classical “Newtonian” physics still remain accurate in predicting the behavior of surrounding (“large”) objects—of the order of the size of large molecules and bigger—at velocities much smaller than the velocity of light.
Theory
There are numerous mathematically equivalent formulations of quantum mechanics. One of the oldest and most commonly used formulations is the transformation theory proposed by Cambridge theoretical physicist Paul Dirac, which unifies and generalizes the two earliest formulations of quantum mechanics, matrix mechanics (invented by Werner Heisenberg)[2] and wave mechanics (invented by Erwin Schrödinger).
In this formulation, the instantaneous state of a quantum system encodes the probabilities of its measurable properties, or "observables". Examples of observables include energy, position, momentum, and angular momentum. Observables can be either continuous (e.g., the position of a particle) or discrete (e.g., the energy of an electron bound to a hydrogen atom).
Generally, quantum mechanics does not assign definite values to observables. Instead, it makes predictions about probability distributions; that is, the probability of obtaining each of the possible outcomes from measuring an observable. Naturally, these probabilities will depend on the quantum state at the instant of the measurement. There are, however, certain states that are associated with a definite value of a particular observable. These are known as "eigenstates" of the observable ("eigen" can be roughly translated from German as inherent or as a characteristic). In the everyday world, it is natural and intuitive to think of everything being in an eigenstate of every observable. Everything appears to have a definite position, a definite momentum, and a definite time of occurrence. However, quantum mechanics does not pinpoint the exact values for the position or momentum of a certain particle in a given space in a finite time; rather, it only provides a range of probabilities of where that particle might be. Therefore, it became necessary to use different words for (a) the state of something having an uncertainty relation and (b) a state that has a definite value. The latter is called the "eigenstate" of the property being measured.
For example, consider a free particle. In quantum mechanics, there is wave-particle duality so the properties of the particle can be described as a wave. Therefore, its quantum state can be represented as a wave, of arbitrary shape and extending over all of space, called a wave function. The position and momentum of the particle are observables. The Uncertainty Principle of quantum mechanics states that both the position and the momentum cannot simultaneously be known with infinite precision at the same time. However, one can measure just the position alone of a moving free particle creating an eigenstate of position with a wavefunction that is very large at a particular position x, and almost zero everywhere else. If one performs a position measurement on such a wavefunction, the result x will be obtained with almost 100% probability. In other words, the position of the free particle will almost be known. This is called an eigenstate of position (mathematically more precise: a generalized eigenstate (eigendistribution) ). If the particle is in an eigenstate of position then its momentum is completely unknown. An eigenstate of momentum, on the other hand, has the form of a plane wave. It can be shown that the wavelength is equal to h/p, where h is Planck's constant and p is the momentum of the eigenstate. If the particle is in an eigenstate of momentum then its position is completely blurred out.
Usually, a system will not be in an eigenstate of whatever observable we are interested in. However, if one measures the observable, the wavefunction will instantaneously be an eigenstate (or generalized eigenstate) of that observable. This process is known as wavefunction collapse. It involves expanding the system under study to include the measurement device, so that a detailed quantum calculation would no longer be feasible and a classical description must be used. If one knows the corresponding wave function at the instant before the measurement, one will be able to compute the probability of collapsing into each of the possible eigenstates. For example, the free particle in the previous example will usually have a wavefunction that is a wave packet centered around some mean position x0, neither an eigenstate of position nor of momentum. When one measures the position of the particle, it is impossible to predict with certainty the result that we will obtain. It is probable, but not certain, that it will be near x0, where the amplitude of the wave function is large. After the measurement is performed, having obtained some result x, the wave function collapses into a position eigenstate centered at x.
Wave functions can change as time progresses. An equation known as the Schrödinger equation describes how wave functions change in time, a role similar to Newton's second law in classical mechanics. The Schrödinger equation, applied to the aforementioned example of the free particle, predicts that the center of a wave packet will move through space at a constant velocity, like a classical particle with no forces acting on it. However, the wave packet will also spread out as time progresses, which means that the position becomes more uncertain. This also has the effect of turning position eigenstates (which can be thought of as infinitely sharp wave packets) into broadened wave packets that are no longer position eigenstates.
Some wave functions produce probability distributions that are constant in time. Many systems that are treated dynamically in classical mechanics are described by such "static" wave functions. For example, a single electron in an unexcited atom is pictured classically as a particle moving in a circular trajectory around the atomic nucleus, whereas in quantum mechanics it is described by a static, spherically symmetric wavefunction surrounding the nucleus (Fig. 1). (Note that only the lowest angular momentum states, labeled s, are spherically symmetric).
The time evolution of wave functions is deterministic in the sense that, given a wavefunction at an initial time, it makes a definite prediction of what the wavefunction will be at any later time. During a measurement, the change of the wavefunction into another one is not deterministic, but rather unpredictable, i.e., random.
The probabilistic nature of quantum mechanics thus stems from the act of measurement. This is one of the most difficult aspects of quantum systems to understand. It was the central topic in the famous Bohr-Einstein debates, in which the two scientists attempted to clarify these fundamental principles by way of thought experiments. In the decades after the formulation of quantum mechanics, the question of what constitutes a "measurement" has been extensively studied. Interpretations of quantum mechanics have been formulated to do away with the concept of "wavefunction collapse"; see, for example, the relative state interpretation. The basic idea is that when a quantum system interacts with a measuring apparatus, their respective wavefunctions become entangled, so that the original quantum system ceases to exist as an independent entity. For details, see the article on measurement in quantum mechanics.
Mathematical formulation
- See also: Quantum logic
In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac and John von Neumann, the possible states of a quantum mechanical system are represented by unit vectors (called "state vectors") residing in a complex separable Hilbert space (variously called the "state space" or the "associated Hilbert space" of the system) well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system; for example, the state space for position and momentum states is the space of square-integrable functions, while the state space for the spin of a single proton is just the product of two complex planes. Each observable is represented by a maximally-Hermitian (precisely: by a self-adjoint) linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate. If the operator's spectrum is discrete, the observable can only attain those discrete eigenvalues.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During a measurement, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator - which explains the choice of Hermitian operators, for which all the eigenvalues are real. We can find the probability distribution of an observable in a given state by computing the spectral decomposition of the corresponding operator. Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute.
The Schrödinger equation acts on the entire probability amplitude, not merely its absolute value. Whereas the absolute value of the probability amplitude encodes information about probabilities, its phase encodes information about the interference between quantum states. This gives rise to the wave-like behavior of quantum states.
It turns out that analytic solutions of Schrödinger's equation are only available for a small number of model Hamiltonians, of which the quantum harmonic oscillator, the particle in a box, the hydrogen molecular ion and the hydrogen atom are the most important representatives. Even the helium atom, which contains just one more electron than hydrogen, defies all attempts at a fully analytic treatment. There exist several techniques for generating approximate solutions. For instance, in the method known as perturbation theory one uses the analytic results for a simple quantum mechanical model to generate results for a more complicated model related to the simple model by, for example, the addition of a weak potential energy. Another method is the "semi-classical equation of motion" approach, which applies to systems for which quantum mechanics produces weak deviations from classical behavior. The deviations can be calculated based on the classical motion. This approach is important for the field of quantum chaos.
An alternative formulation of quantum mechanics is Feynman's path integral formulation, in which a quantum-mechanical amplitude is considered as a sum over histories between initial and final states; this is the quantum-mechanical counterpart of action principles in classical mechanics.
Interactions with other scientific theories
The fundamental rules of quantum mechanics are very broad. They assert that the state space of a system is a Hilbert space and the observables are Hermitian operators acting on that space, but do not tell us which Hilbert space or which operators, or if it even exists. These must be chosen appropriately in order to obtain a quantitative description of a quantum system. An important guide for making these choices is the correspondence principle, which states that the predictions of quantum mechanics reduce to those of classical physics when a system moves to higher energies or equivalently, larger quantum numbers. In other words, classic mechanics is simply a quantum mechanics of large systems. This "high energy" limit is known as the classical or correspondence limit. One can therefore start from an established classical model of a particular system, and attempt to guess the underlying quantum model that gives rise to the classical model in the correspondence limit.
When quantum mechanics was originally formulated, it was applied to models whose correspondence limit was non-relativistic classical mechanics. For instance, the well-known model of the quantum harmonic oscillator uses an explicitly non-relativistic expression for the kinetic energy of the oscillator, and is thus a quantum version of the classical harmonic oscillator.
Early attempts to merge quantum mechanics with special relativity involved the replacement of the Schrödinger equation with a covariant equation such as the Klein-Gordon equation or the Dirac equation. While these theories were successful in explaining many experimental results, they had certain unsatisfactory qualities stemming from their neglect of the relativistic creation and annihilation of particles. A fully relativistic quantum theory required the development of quantum field theory, which applies quantization to a field rather than a fixed set of particles. The first complete quantum field theory, quantum electrodynamics, provides a fully quantum description of the electromagnetic interaction.
The full apparatus of quantum field theory is often unnecessary for describing electrodynamic systems. A simpler approach, one employed since the inception of quantum mechanics, is to treat charged particles as quantum mechanical objects being acted on by a classical electromagnetic field. For example, the elementary quantum model of the hydrogen atom describes the electric field of the hydrogen atom using a classical  Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Coulomb potential. This "semi-classical" approach fails if quantum fluctuations in the electromagnetic field play an important role, such as in the emission of photons by charged particles.
Quantum field theories for the strong nuclear force and the weak nuclear force have been developed. The quantum field theory of the strong nuclear force is called quantum chromodynamics, and describes the interactions of the subnuclear particles: quarks and gluons. The weak nuclear force and the electromagnetic force were unified, in their quantized forms, into a single quantum field theory known as electroweak theory, by the physicists Abdus Salam, Sheldon Glashow and Steven Weinberg.
It has proven difficult to construct quantum models of gravity, the remaining fundamental force. Semi-classical approximations are workable, and have led to predictions such as Hawking radiation. However, the formulation of a complete theory of quantum gravity is hindered by apparent incompatibilities between general relativity, the most accurate theory of gravity currently known, and some of the fundamental assumptions of quantum theory. The resolution of these incompatibilities is an area of active research, and theories such as string theory are among the possible candidates for a future theory of quantum gravity.
Derivation of quantization
The particle in a 1-dimensional potential energy box is the most simple example where restraints lead to the quantization of energy levels. The box is defined as zero potential energy inside a certain interval and infinite everywhere outside that interval. For the 1-dimensional case in the x direction, the time-independent Schrödinger equation can be written as[3]:
The general solutions are:
or
The presence of the walls of the box restricts the acceptable solutions of the wavefunction. At each wall :
Consider x = 0
- sin 0 = 0, cos 0 = 1. To satisfy
 the cos term has to be removed. Hence D = 0
the cos term has to be removed. Hence D = 0
Now consider: 
- at x = L,

- If C = 0 then
 for all x. This would conflict with the Born interpretation
for all x. This would conflict with the Born interpretation - therefore sin kL = 0 must be satisfied, yielding the condition
In this situation, n must be an integer showing the quantization of the energy levels.
Applications
Quantum mechanics has had enormous success in explaining many of the features of our world. The individual behaviour of the subatomic particles that make up all forms of matter—electrons, protons, neutrons, photons and others—can often only be satisfactorily described using quantum mechanics. Quantum mechanics has strongly influenced string theory, a candidate for a theory of everything (see reductionism) and the multiverse hypothesis. It is also related to statistical mechanics.
Quantum mechanics is important for understanding how individual atoms combine covalently to form chemicals or molecules. The application of quantum mechanics to chemistry is known as quantum chemistry. (Relativistic) quantum mechanics can in principle mathematically describe most of chemistry. Quantum mechanics can provide quantitative insight into ionic and covalent bonding processes by explicitly showing which molecules are energetically favorable to which others, and by approximately how much. Most of the calculations performed in computational chemistry rely on quantum mechanics.
Much of modern technology operates at a scale where quantum effects are significant. Examples include the laser, the transistor, the electron microscope, and magnetic resonance imaging. The study of semiconductors led to the invention of the diode and the transistor, which are indispensable for modern electronics.
Researchers are currently seeking robust methods of directly manipulating quantum states. Efforts are being made to develop quantum cryptography, which will allow guaranteed secure transmission of information. A more distant goal is the development of quantum computers, which are expected to perform certain computational tasks exponentially faster than classical computers. Another active research topic is quantum teleportation, which deals with techniques to transmit quantum states over arbitrary distances.
In many devices, even the simple light switch, quantum tunneling is vital, as otherwise the electrons in the electric current could not penetrate the potential barrier made up, in the case of the light switch, of a layer of oxide. Flash memory chips found in USB drives also use quantum tunneling to erase their memory cells.
Philosophical consequences
-
- Main article: Interpretation of quantum mechanics
Since its inception, the many counter-intuitive results of quantum mechanics have provoked strong philosophical debate and many interpretations. Even fundamental issues such as Max Born's basic rules concerning probability amplitudes and probability distributions took decades to be appreciated.
The Copenhagen interpretation, due largely to the Danish theoretical physicist Niels Bohr, is the interpretation of quantum mechanics most widely accepted amongst physicists. According to it, the probabilistic nature of quantum mechanics predictions cannot be explained in terms of some other deterministic theory, and does not simply reflect our limited knowledge. Quantum mechanics provides probabilistic results because the physical universe is itself probabilistic rather than deterministic.
Albert Einstein, himself one of the founders of quantum theory, disliked this loss of determinism in measurement. (Hence his famous quote "God does not play dice with the universe.") He held that there should be a local hidden variable theory underlying quantum mechanics and consequently the present theory was incomplete. He produced a series of objections to the theory, the most famous of which has become known as the EPR paradox. John Bell showed that the EPR paradox led to experimentally testable differences between quantum mechanics and local realistic theories. Experiments have been performed confirming the accuracy of quantum mechanics, thus demonstrating that the physical world cannot be described by local realistic theories.
The writer C. S. Lewis viewed quantum mechanics as incomplete. Lewis, a professor of English, was of the opinion that the Heisenberg uncertainty principle was more of an epistemic limitation than an indication of ontological indeterminacy, and in this respect believed similarly to many advocates of hidden variables theories.[citation needed] The Bohr-Einstein debates provide a vibrant critique of the Copenhagen Interpretation from an epistemological point of view.
The Everett many-worlds interpretation, formulated in 1956, holds that all the possibilities described by quantum theory simultaneously occur in a "multiverse" composed of mostly independent parallel universes. This is not accomplished by introducing some new axiom to quantum mechanics, but on the contrary by removing the axiom of the collapse of the wave packet: All the possible consistent states of the measured system and the measuring apparatus (including the observer) are present in a real physical (not just formally mathematical, as in other interpretations) quantum superposition. (Such a superposition of consistent state combinations of different systems is called an entangled state.) While the multiverse is deterministic, we perceive non-deterministic behavior governed by probabilities, because we can observe only the universe, i.e. the consistent state contribution to the mentioned superposition, we inhabit. Everett's interpretation is perfectly consistent with John Bell's experiments and makes them intuitively understandable. However, according to the theory of quantum decoherence, the parallel universes will never be accessible to us. This inaccessibility can be understood as follows: once a measurement is done, the measured system becomes entangled with both the physicist who measured it and a huge number of other particles, some of which are photons flying away towards the other end of the universe; in order to prove that the wave function did not collapse one would have to bring all these particles back and measure them again, together with the system that was measured originally. This is completely impractical, but even if one can theoretically do this, it would destroy any evidence that the original measurement took place (including the physicist's memory).
General relativity

| General relativity | ||||||
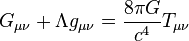 | ||||||
| Einstein field equations | ||||||
| Introduction to...
Mathematical formulation of... Resources
| ||||||
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the state-of-the art description of gravity in modern physics. It unifies special relativity and Newton's law of universal gravitation, and describes gravity as a property of the geometry of space and time, or spacetime. In particular, the curvature of spacetime is directly related to the four-momentum (mass-energy and linear momentum) of whatever matter and radiation are present. The relation is specified by the Einstein field equations, a system of partial differential equations.
The predictions of general relativity differ significantly from those of classical physics, especially concerning the passage of time, the geometry of space, the motion of bodies in free fall, and the propagation of light. Examples of such differences include gravitational time dilation, the gravitational redshift of light, and the gravitational time delay. General relativity's predictions have been confirmed in all observations and experiments to date. Although general relativity is not the only relativistic theory of gravity, it is the simplest theory that is consistent with experimental data. However, unanswered questions remain, the most fundamental being how general relativity can be reconciled with the laws of quantum physics to produce a complete and self-consistent theory of quantum gravity.
Einstein's theory has important astrophysical applications. It points towards the existence of black holes—regions of space in which space and time are distorted in such a way that nothing, not even light, can escape—as an end-state for massive stars. There is evidence that such stellar black holes as well as more massive varieties of black hole are responsible for the intense radiation emitted by certain types of astronomical objects such as active galactic nuclei or microquasars. The bending of light by gravity can lead to the phenomenon of gravitational lensing, where multiple images of the same distant astronomical object are visible in the sky. General relativity also predicts the existence of gravitational waves, which have since been measured indirectly; a direct measurement is the aim of projects such as LIGO. In addition, general relativity is the basis of current cosmological models of an expanding universe.
Contents |
History
Soon after publishing the special theory of relativity in 1905, Einstein started thinking about how to incorporate gravity into his new relativistic framework. In 1907, beginning with a simple thought experiment involving an observer in free fall, he embarked on what would be an eight-year search for a relativistic theory of gravity. After numerous detours and false starts, his work culminated in the November, 1915 presentation to the Prussian Academy of Science of what are now known as the Einstein field equations. These equations specify how the geometry of space and time is influenced by whatever matter is present, and form the core of Einstein's general theory of relativity.[1]
The Einstein field equations are nonlinear and very difficult to solve. Einstein used approximation methods in working out initial predictions of the theory. But as early as 1916, the astrophysicist Karl Schwarzschild found the first non-trivial exact solution to the Einstein field equations, the so-called Schwarzschild metric. This solution laid the groundwork for the description of the final stages of gravitational collapse, and the objects known today as black holes. In the same year, the first steps towards generalizing Schwarzschild's solution to electrically charged objects were taken, which eventually resulted in the Reissner-Nordström solution, now associated with charged black holes.[2] In 1917, Einstein applied his theory to the universe as a whole, initiating the field of relativistic cosmology. In line with contemporary thinking, he assumed a static universe, adding a new parameter to his original field equations—the cosmological constant—to reproduce that "observation".[3] By 1929, however, the work of Hubble and others had shown that our universe is expanding. This is readily described by the expanding cosmological solutions found by Friedmann in 1922, which do not require a cosmological constant. Lemaître used these solutions to formulate the earliest version of the big bang models, in which our universe has evolved from an extremely hot and dense earlier state.[4] Einstein later declared the cosmological constant the biggest blunder of his life.[5]
During that period, general relativity remained something of a curiosity among physical theories. It was clearly superior to Newtonian gravity, being consistent with special relativity and accounting for several effects unexplained by the Newtonian theory. Einstein himself had shown in 1915 how his theory explained the anomalous perihelion advance of the planet Mercury without any arbitrary parameters ("fudge factors").[6] Similarly, a 1919 expedition led by Eddington confirmed general relativity's prediction for the deflection of starlight by the Sun,[7] making Einstein instantly famous.[8] Yet the theory entered the mainstream of theoretical physics and astrophysics only with the developments between approximately 1960 and 1975, now known as the Golden age of general relativity. Physicists began to understand the concept of a black hole, and to identify these objects' astrophysical manifestation as quasars.[9] Ever more precise solar system tests confirmed the theory's predictive power,[10] and relativistic cosmology, too, became amenable to direct observational tests.[11]
From classical mechanics to general relativity
General relativity is best understood by examining its similarities with and departures from classical physics. The first step is the realization that classical mechanics and Newton's law of gravity admit of a geometric description. The combination of this description with the laws of special relativity results in a heuristic derivation of general relativity.[12]
Geometry of Newtonian gravity
At the base of classical mechanics is the notion that a body's motion can be described as a combination of free (or inertial) motion, and deviations from this free motion. Such deviations are caused by external forces acting on a body in accordance with Newton's second law of motion, which states that the total force acting on a body is equal to that body's (inertial) mass times its acceleration.[13] The preferred inertial motions are related to the geometry of space and time: in the standard reference frames of classical mechanics, objects in free motion move along straight lines at constant speed. In modern parlance, their paths are geodesics, straight world lines in spacetime.[14]
Conversely, one might expect that inertial motions, once identified by observing the actual motions of bodies and making allowances for the external forces (such as electromagnetism or friction), can be used to define the geometry of space, as well as a time coordinate. However, there is an ambiguity once gravity comes into play. According to Newton's law of gravity, and independently verified by experiments such as that of Eötvös and its successors (see Eötvös experiment) , there is a universality of free fall (also known as the weak equivalence principle, or the universal equality of inertial and passive-gravitational mass): the trajectory of a test body in free fall depends only on its position and initial speed, but not on any of its material properties.[15] A simplified version of this is embodied in Einstein's elevator experiment, illustrated in the figure on the right: for an observer in a small enclosed room, it is impossible to decide, by mapping the trajectory of bodies such as a dropped ball, whether the room is at rest in a gravitational field, or in free space aboard an accelerated rocket.[16]
Given the universality of free fall, there is no observable distinction between inertial motion and motion under the influence of the gravitational force. This suggests the definition of a new class of inertial motion, namely that of objects in free fall under the influence of gravity. This new class of preferred motions, too, defines a geometry of space and time—in mathematical terms, it is the geodesic motion associated with a specific connection which depends on the gradient of the gravitational potential. Space, in this construction, still has the ordinary Euclidean geometry. However, spacetime as a whole is more complicated. As can be shown using simple thought experiments following the free-fall trajectories of different test particles, the result of transporting spacetime vectors that can denote a particle's velocity (time-like vectors) will vary with the particle's trajectory; mathematically speaking, the Newtonian connection is not integrable. From this, one can deduce that spacetime is curved. The result is a geometric formulation of Newtonian gravity using only covariant concepts, i.e. a description which is valid in any desired coordinate system.[17] In this geometric description, tidal effects—the relative acceleration of bodies in free fall—are related to the derivative of the connection, showing how the modified geometry is caused by the presence of mass.[18]
Relativistic generalization
As intriguing as geometric Newtonian gravity may be, its basis, classical mechanics, is merely a limiting case of (special) relativistic mechanics.[19] In the language of symmetry: where gravity can be neglected, physics is Lorentz invariant as in special relativity rather than Galilei invariant as in classical mechanics. (The defining symmetry of special relativity is the Poincaré group which also includes translations and rotations.) The differences between the two become significant when we are dealing with speeds approaching the speed of light, and with high-energy phenomena.[20]
With Lorentz symmetry, additional structures comes into play. They are defined by the set of light cones (see the image on the left). The light-cones define a causal structure: for each event A, there is a set of events that can, in principle, either influence or be influenced by A via signals or interactions that do not need to travel faster than light (such as event B in the image), and a set of events for which such an influence is impossible (such as event C in the image). These sets are observer-independent.[21] In conjunction with the world-lines of freely falling particles, the light-cones can be used to reconstruct the space-time's semi-Riemannian metric, at least up to a positive scalar factor. In mathematical terms, this defines a conformal structure.[22]
Special relativity is defined in the absence of gravity, so for practical applications, it is a suitable model whenever gravity can be neglected. Bringing gravity into play, and assuming the universality of free fall, an analogous reasoning as in the previous section applies: there are no global inertial frames. Instead there are approximate inertial frames moving alongside freely falling particles. Translated into the language of spacetime: the straight time-like lines that define a gravity-free inertial frame are deformed to lines that are curved relative to each other, suggesting that the inclusion of gravity necessitates a change in spacetime geometry.[23]
A priori, it is not clear whether the new local frames in free fall coincide with the reference frames in which the laws of special relativity hold—that theory is based on the propagation of light, and thus on electromagnetism, which could have a different set of preferred frames. But using different assumptions about the special-relativistic frames (such as their being earth-fixed, or in free fall), one can derive different predictions for the gravitational redshift, that is, the way in which the frequency of light shifts as the light propagates through a gravitational field (cf. below). The actual measurements show that free-falling frames are the ones in which light propagates as it does in special relativity.[24] The generalization of this statement, namely that the laws of special relativity hold to good approximation in freely falling (and non-rotating) reference frames, is known as the Einstein equivalence principle, a crucial guiding principle for generalizing special-relativistic physics to include gravity.[25]
The same experimental data shows that time as measured by clocks in a gravitational field—proper time, to give the technical term—does not follow the rules of special relativity. In the language of spacetime geometry, it is not measured by the Minkowski metric. As in the Newtonian case, this is suggestive of a more general geometry. At small scales, all reference frames that are in free fall are equivalent, and approximately Minkowskian. Consequently, we are now dealing with a curved generalization of Minkowski space. The metric tensor that defines the geometry—in particular, how lengths and angles are measured—is not the Minkowski metric of special relativity, it is a generalization known as a semi- or pseudo-Riemannian metric. Furthermore, each Riemannian metric is naturally associated with one particular kind of connection, the Levi-Civita connection, and this is, in fact, the connection that satisfies the equivalence principle and makes space locally Minkowskian (that is, in suitable "locally inertial" coordinates, the metric is Minkowskian, and its derivatives and the connection coefficients vanish).[26]
Einstein's equations
Having formulated the relativistic, geometric version of the effects of gravity, the question of gravity's source remains. In Newtonian gravity, the source is mass. In special relativity, mass turns out to be part of a more general quantity called the energy-momentum tensor, which includes both energy and momentum densities as well as stress (that is, pressure and shear).[27] Using the equivalence principle, this tensor is readily generalized to curved space-time. Drawing further upon the analogy with geometric Newtonian gravity, it is natural to assume that the field equation for gravity relates this tensor and the Ricci tensor, which describes a particular class of tidal effects: the change in volume for a small cloud of test particles that are initially at rest, and then fall freely. In special relativity, conservation of energy-momentum corresponds to the statement that the energy-momentum tensor is divergence-free. This formula, too, is readily generalized to curved spacetime by replacing partial derivatives with their curved-manifold counterparts, covariant derivatives studied in differential geometry. With this additional condition—the covariant divergence of the energy-momentum tensor, and hence of whatever is on the other side of the equation, is zero— the simplest set of equations are what are called Einstein's (field) equations:
On the left-hand side is a specific divergence-free combination of the Ricci tensor Rab and the metric known as the Einstein tensor. In particular,
is the curvature scalar. The Ricci tensor itself is related to the more general Riemann curvature tensor as
On the right-hand side, Tab is the energy-momentum tensor. All tensors are written in abstract index notation.[28] Matching the theory's prediction to observational results for planetary orbits (or, equivalently, assuring that the weak-gravity, low-speed limit is Newtonian mechanics), the proportionality constant can be fixed as κ = 8πG/c4, with G the gravitational constant and c the speed of light.[29] When there is no matter present, so that the energy-momentum tensor vanishes, the result are the vacuum Einstein equations,
There are alternatives to general relativity built upon the same premises, which include additional rules and/or constraints, leading to different field equations. Examples are Brans-Dicke theory, teleparallelism, and Einstein-Cartan theory.[30]
Definition and basic applications
The derivation outlined in the previous section contains all the information needed to define general relativity, describe its key properties, and address a question of crucial importance in physics, namely how the theory can be used for model-building.
Definition and basic properties
General relativity is a metric theory of gravitation. At its core are Einstein's equations, which describe the relation between the geometry of a four-dimensional, semi-Riemannian manifold representing spacetime on the one hand, and the energy-momentum contained in that spacetime on the other.[31] Phenomena that in classical mechanics are ascribed to the action of the force of gravity (such as free-fall, orbital motion, and spacecraft trajectories), correspond to inertial motion within a curved geometry of spacetime in general relativity; there is no gravitational force deflecting objects from their natural, straight paths. Instead, gravity corresponds to changes in the properties of space and time, which in turn changes the straightest-possible paths that objects will naturally follow.[32] The curvature is, in turn, caused by the energy-momentum of matter. Paraphrasing the relativist John Archibald Wheeler, spacetime tells matter how to move; matter tells spacetime how to curve.[33]
While general relativity replaces the scalar gravitational potential of classical physics by a symmetric rank-two tensor, the latter reduces to the former in certain limiting cases. For weak gravitational fields and slow speed relative to the speed of light, the theory's predictions converge on those of Newton's law of gravity.[34]
As it is constructed using tensors, general relativity exhibits general covariance: its laws—and further laws formulated within the general relativistic framework—take on the same form in all coordinate systems.[35] Furthermore, the theory does not contain any invariant geometric background structures. It thus satisfies a more stringent general principle of relativity, namely that the laws of physics are the same for all observers.[36] Locally, as expressed in the equivalence principle, spacetime is Minkowskian, and the laws of physics exhibit local Lorentz invariance.[37]
Model-building
The core concept of general-relativistic model-building is that of a solution of Einstein's equations. Given both Einstein's equations and suitable equations for the properties of matter, such a solution consists of a specific semi-Riemannian manifold (usually defined by giving the metric in specific coordinates), and specific matter fields defined on that manifold. Matter and geometry must satisfy Einstein's equations, so in particular, the matter's energy-momentum tensor must be divergence-free. The matter must, of course, also satisfy wheatever additional equations were imposed on its properties. In short, such a solution is a model universe that satisfies the laws of general relativity, and possibly additional laws governing whatever matter might be present.[38]
Einstein's equations are nonlinear partial differential equations and, as such, difficult to solve exactly.[39] Nevertheless, a number of exact solutions are known, although only a few have direct physical applications.[40] The best-known exact solutions, and also those most interesting from a physics point of view, are the Schwarzschild solution, the Reissner-Nordström solution and the Kerr metric, each corresponding to a certain type of black hole in an otherwise empty universe,[41] and the Friedmann-Lemaître-Robertson-Walker and de Sitter universes, each describing an expanding cosmos.[42] Exact solutions of great theoretical interest include the Gödel universe (which opens up the intriguing possibility of time travel in curved spacetimes), the Taub-NUT solution (a model universe that is homogeneous, but anisotropic), and Anti-de Sitter space (which has recently come to prominence in the context of what is called the Maldacena conjecture).[43]
Given the difficulty of finding exact solutions, Einstein's field equations are also solved frequently by numerical integration on a computer, or by considering small perturbations of exact solutions. In the field of numerical relativity, powerful computers are employed to simulate the geometry of spacetime and to solve Einstein's equations for interesting situations such as two colliding black holes.[44] In principle, such methods may be applied to any system, given sufficient computer resources, and may address fundamental questions such as naked singularities. Approximate solutions may also be found by perturbation theories such as linearized gravity[45] and its generalization, the post-Newtonian expansion, both of which were developed by Einstein. The latter provides a systematic approach to solving for the geometry of a spacetime that contains a distribution of matter that moves slowly compared with the speed of light. The expansion involves a series of terms; the first terms represent Newtonian gravity, whereas the later terms represent ever smaller corrections to Newton's theory due to general relativity.[46] An extension of this expansion is the parametrized post-Newtonian (PPN) formalism, which allows quantitative comparisons between the predictions of general relativity and alternative theories.[47]
Consequences of Einstein's theory
General relativity has a number of physical consequences. Some follow directly from the theory's axioms, whereas others have become clear only in the course of the ninety years of research that followed Einstein's initial publication.
Gravitational time dilation and frequency shift
Assuming that the equivalence principle holds,[48] gravity influences the passage of time. Light sent down into a gravity well is blueshifted, whereas light sent in the opposite direction (i.e., climbing out of the gravity well) is redshifted; collectively, these two effects are known as the gravitational frequency shift. More generally, processes close to a massive body run more slowly when compared with processes taking place further away; this effect is known as gravitational time dilation.[49]
Gravitational redshift has been measured in the laboratory[50] and using astronomical observations.[51] Gravitational time dilation in the Earth's gravitational field has been measured numerous times using atomic clocks,[52] while ongoing validation is provided as a side-effect of the operation of the Global Positioning System (GPS).[53] Tests in stronger gravitational fields are provided by the observation of binary pulsars.[54] All results are in agreement with general relativity.[55] However, at the current level of accuracy, these observations cannot distinguish between general relativity and other theories in which the equivalence principle is valid.[56]
Light deflection and gravitational time delay
General relativity predicts that the path of light is bent in a gravitational field; light passing a massive body is deflected towards that body. This effect has been confirmed by observing the light of stars or distant quasars being deflected as it passes the Sun.[57]
This and related predictions follow from the fact that light follows what is called a light-like or null geodesic—a generalization of the straight lines along which light travels in classical physics. Such geodesics are the generalization of the invariance of lightspeed in special relativity.[58] As one examines suitable model spacetimes (either the exterior Schwarzschild solution or, for more than a single mass, the post-Newtonian expansion),[59] several effects of gravity on light propagation emerge. Although the bending of light can also be derived by extending the universality of free fall to light,[60] the angle of deflection resulting from such calculations is only half the value given by general relativity.[61]
Closely related to light deflection is the gravitational time delay (or Shapiro effect), the phenomenon that light signals take longer to move through a gravitational field than they would in the absence of that field. There have been numerous successful tests of this prediction.[62] In the parameterized post-Newtonian formalism (PPN), measurements of both the deflection of light and the gravitational time delay determine a parameter called γ, which encodes the influence of gravity on the geometry of space.[63]
Gravitational waves
One of several analogies between weak-field gravity and electromagnetism is that, analogous to electromagnetic waves, there are gravitational waves: ripples in the metric of spacetime that propagate at the speed of light.[64] The simplest type of such a wave can be visualized by its action on a ring of freely floating particles (upper image to the right). A sine wave propagating through such a ring towards the reader distorts the ring in a characteristic, rhythmic fashion (lower, animated image to the right).[65] Since Einstein's equations are non-linear, arbitrarily strong gravitational waves do not obey linear superposition, making their description difficult. However, for weak fields, a linear approximation can be made. Such linearized gravitational waves are sufficiently accurate to describe the exceedingly weak waves that are expected to arrive here on Earth from far-off cosmic events, which typically result in relative distances increasing and decreasing by 10 − 21 or less. Data-analysis methods routinely make use of the fact that these linearized waves can be Fourier decomposed.[66]
Some exact solutions describe gravitational waves without any approximation, e.g., a wave train traveling through empty space[67] or so-called Gowdy universes, varieties of an expanding cosmos filled with gravitational waves.[68] But for gravitational waves produced in astrophysically relevant situations, such as the merger of two black holes, numerical methods are presently the only way to construct appropriate models.[69]
Orbital effects and the relativity of direction
General relativity differs from classical mechanics in a number of predictions concerning orbiting bodies. It predicts an overall rotation (precession) of planetary orbits, as well as orbital decay caused by the emission of gravitational waves and effects related to the relativity of direction.
[edit] Precession of apsides
In general relativity, the apsides of any orbit (the point of the orbiting body's closest approach to the system's center of mass) will precess—the orbit is not an ellipse, but akin to an ellipse that rotates on its focus, resulting in a rose curve-like shape (see image). Einstein first derived this result by using an approximate metric representing the Newtonian limit and treating the orbiting body as a test particle. For him, the fact that his theory gave a straightforward explanation of the anomalous perihelion shift of the planet Mercury, discovered earlier by Urbain Le Verrier in 1859, was important evidence that he had at last identified the correct form of the gravitational field equations.[70]
The effect can also be derived by using either the exact Schwarzschild metric (describing spacetime around a spherical mass)[71] or the much more general post-Newtonian formalism.[72] It is due to the influence of gravity on the geometry of space and to the contribution of self-energy to a body's gravity (encoded in the nonlinearity of Einstein's equations).[73] Relativistic precession has been observed for all planets that allow for accurate precession measurements (Mercury, Venus and the Earth),[74] as well as in binary pulsar systems, where it is larger by five orders of magnitude.[75]
Orbital decay

According to general relativity, a binary system will emit gravitational waves, thereby losing energy. Due to this loss, the distance between the two orbiting bodies decreases, and so does their orbital period. Within the solar system or for ordinary double stars, the effect is too small to be observable. Not so for a close binary pulsar, a system of two orbiting neutron stars, one of which is a pulsar: from the pulsar, observers on Earth receive a regular series of radio pulses that can serve as a highly accurate clock, which allows precise measurements of the orbital period. Since the neutron stars are very compact, significant amounts of energy are emitted in the form of gravitational radiation.[77]
The first observation of a decrease in orbital period due to the emission of gravitational waves was made by Hulse and Taylor, using the binary pulsar PSR1913+16 they had discovered in 1974. This was the first detection of gravitational waves, albeit indirect, for which they were awarded the 1993 Nobel Prize in physics.[78] Since then, several other binary pulsars have been found, in particular the double pulsar PSR J0737-3039, in which both stars are pulsars.[79]
Geodetic precession and frame-dragging
Several relativistic effects are directly related to the relativity of direction.[80] One is geodetic precession: the axis direction of a gyroscope in free fall in curved spacetime will change when compared, for instance, with the direction of light received from distant stars—even though such a gyroscope represents the way of keeping a direction as stable as possible ("parallel transport").[81] For the Moon-Earth-system, this effect has been measured with the help of lunar laser ranging.[82] More recently, it has been measured for test masses aboard the satellite Gravity Probe B to a precision of better than 1 percent.[83]
Near a rotating mass, there are so-called gravitomagnetic or frame-dragging effects. A distant observer will determine that objects close to the mass get "dragged around". This is most extreme for rotating black holes where, for any object entering a zone known as the ergosphere, rotation is inevitable.[84] Such effects can again be tested through their influence on the orientation of gyroscopes in free fall.[85] Somewhat controversial tests have been performed using the LAGEOS satellites, confirming the relativistic prediction.[86] A precision measurement is the main aim of the Gravity Probe B mission, with the results expected in September 2008.[87]
Astrophysical applications
Gravitational lensing
The deflection of light by gravity is responsible for a new class of astronomical phenomena. If a massive object is situated between the astronomer and a distant target object with appropriate mass and relative distances, the astronomer will see multiple distorted images of the target. Such effects are known as gravitational lensing.[88] Depending on the configuration, scale, and mass distribution, there can be two or more images, a bright ring known as an Einstein ring, or partial rings called arcs.[89] The earliest example was discovered in 1979;[90] since then, more than a hundred gravitational lenses have been observed.[91] Even if the multiple images are too close to each other to be resolved, the effect can still be measured, e.g., as an overall brightening of the target object; a number of such "microlensing events" has been observed.[92]
Gravitational lensing has developed into a tool of observational astronomy. It is used to detect the presence and distribution of dark matter, provide a "natural telescope" for observing distant galaxies, and to obtain an independent estimate of the Hubble constant. Statistical evaluations of lensing data provide valuable insight into the structural evolution of galaxies.[93]
[edit] Gravitational wave astronomy
Observations of binary pulsars provide strong indirect evidence for the existence of gravitational waves (see Orbital decay, above). However, gravitational waves reaching us from the depths of the cosmos have not been detected directly, which is a major goal of current relativity-related research.[94] Several land-based gravitational wave detectors are currently in operation, most notably the interferometric detectors GEO 600, LIGO (three detectors), TAMA 300 and VIRGO.[95] A joint US-European space-based detector, LISA, is currently under development,[96] with a precursor mission (LISA Pathfinder) due for launch in late 2009.[97]
Observations of gravitational waves promise to complement observations in the electromagnetic spectrum.[98] They are expected to yield information about black holes and other dense objects such as neutron stars and white dwarfs, about certain kinds of supernova implosions, and about processes in the very early universe, including the signature of certain types of hypothetical cosmic string.[99]
Black holes and other compact objects
Whenever an object becomes sufficiently compact, general relativity predicts the formation of a black hole, a region of space from which nothing, not even light, can escape. In the currently accepted models of stellar evolution, neutron stars with around 1.4 solar mass and so-called stellar black holes with a few to a few dozen solar masses are thought to be the final state for the evolution of massive stars.[100] Supermassive black holes with a few million to a few billion solar masses are considered the rule rather than the exception in the centers of galaxies,[101] and their presence is thought to have played an important role in the formation of galaxies and larger cosmic structures.[102]
Astronomically, the most important property of compact objects is that they provide a superbly efficient mechanism for converting gravitational energy into electromagnetic radiation.[103] Accretion, the falling of dust or gaseous matter onto stellar or supermassive black holes, is thought to be responsible for some spectacularly luminous astronomical objects, notably diverse kinds of active galactic nuclei on galactic scales and stellar-size objects such as microquasars.[104] In particular, accretion can lead to relativistic jets, focused beams of highly energetic particles that are being flung into space at almost light speed.[105] General relativity plays a central role in modelling all these phenomena,[106] and observations provide strong evidence for the existence of black holes with the properties predicted by the theory.[107]
Black holes are also sought-after targets in the search for gravitational waves (cf. Gravitational waves, above). Merging black hole binaries should lead to some of the strongest gravitational wave signals reaching detectors here on Earth, and the phase directly before the merger ("chirp") could be used as a "standard candle" to deduce the distance to the merger events–and hence serve as a probe of cosmic expansion at large distances.[108] The gravitational waves produced as a stellar black hole plunges into a supermassive one should provide direct information about supermassive black hole's geometry.[109]
Cosmology
The current models of cosmology are based on Einstein's equations including cosmological constant Λ, which has important influence on the large-scale dynamics of the cosmos,
where gab is the spacetime metric.[110] Isotropic and homogeneous solutions of these enhanced equations, the Friedmann-Lemaître-Robertson-Walker solutions,[111] allow physicists to model a universe that has evolved over the past 14 billion years from a hot, early Big Bang phase.[112] Once a small number of parameters (for example the universe's mean matter density) have been fixed by astronomical observation,[113] further observational data can be used to put the models to the test.[114] Predictions, all successful, include the initial abundance of chemical elements formed in a period of primordial nucleosynthesis,[115] the large-scale structure of the universe,[116] and the existence and properties of a "thermal echo" from the early cosmos, the cosmic background radiation.[117]
Astronomical observations of the cosmological expansion rate allow the total amount of matter in the universe to be estimated, although the nature of that matter remains mysterious in part. About 90 percent of all matter appears to be so-called dark matter, which has mass (or, equivalently, gravitational influence), but does not interact electromagnetically and, hence, cannot be observed directly.[118] There is no generally accepted description of this new kind of matter, within the framework of known particle physics[119] or otherwise.[120] Observational evidence from redshift surveys of distant supernovae and measurements of the cosmic background radiation also show that the evolution of our universe is significantly influenced by a cosmological constant resulting in an acceleration of cosmic expansion or, equivalently, by a form of energy with an unusual equation of state, known as dark energy, the nature of which remains unclear.[121]
A so-called inflationary phase,[122] an additional phase of strongly accelerated expansion at cosmic times of around 10 − 33 seconds, was hypothesized in 1980 to account for several puzzling observations that were unexplained by classical cosmological models, such as the nearly perfect homogeneity of the cosmic background radiation.[123] Recent measurements of the cosmic background radiation have resulted in the first evidence for this scenario.[124] However, there is a bewildering variety of possible inflationary scenarios, which cannot be not restricted by current observations.[125] An even larger question is the physics of the earliest universe, prior to the inflationary phase and close to where the classical models predict the big bang singularity. An authoritative answer would require a complete theory of quantum gravity, which has not yet been developed[126] (cf. the section on quantum gravity, below).
Advanced concepts
Causal structure and global geometry

In general relativity, no material body can catch up with or overtake a light pulse. No influence from an event A can reach any other location X before light sent out at A to X. In consequence, an exploration of all light worldlines (null geodesics) yields key information about the spacetime's causal structure. This structure can be displayed using Penrose-Carter diagrams in which infinitely large regions of space and infinite time intervals are shrunk ("compactified") so as to fit onto a finite map, while light still travels along diagonals as in standard spacetime diagrams.[127]
Aware of the importance of causal structure, Roger Penrose and others developed what is known as global geometry. In global geometry, the object of study is not one particular solution (or family of solutions) to Einstein's equations. Rather, relations that hold true for all geodesics, such as the Raychaudhuri equation, and additional non-specific assumptions about the nature of matter (usually in the form of so-called energy conditions) are used to derive general results.[128]
Horizons
Using global geometry, some spacetimes can be shown to contain boundaries called horizons, which demarcate one region from the rest of spacetime. The best-known examples are black holes: if mass is compressed into a sufficiently compact region of space (as specified in the hoop conjecture, the relevant length scale is the Schwarzschild radius[129]), no light from inside can escape to the outside. Since no object can overtake a light pulse, all interior matter is imprisoned as well. Passage from the exterior to the interior is still possible, showing that the boundary, the black hole's horizon, is not a physical barrier.[130]

Early studies of black holes relied on explicit solutions of Einstein's equations, notably the spherically-symmetric Schwarzschild solution (used to describe a static black hole) and the axisymmetric Kerr solution (used to describe a rotating, stationary black hole, and introducing interesting features such as the ergosphere). Using global geometry, later studies have revealed more general properties of black holes. In the long run, they are rather simple objects characterized by eleven parameters specifying energy, linear momentum, angular momentum, location at a specified time and electric charge. This is stated by the black hole uniqueness theorems: "black holes have no hair", that is, no distinguishing marks like the hairstyles of humans. Irrespective of the complexity of a gravitating object collapsing to form a black hole, the object that results (having emitted gravitational waves) is very simple.[131]
Even more remarkably, there is a general set of laws known as black hole mechanics, which is analogous to the laws of thermodynamics. For instance, by the second law of black hole mechanics, the area of the event horizon of a general black hole will never decrease with time, analogous to the entropy of a thermodynamic system. This limits the energy that can be extracted by classical means from a rotating black hole (e.g. by the Penrose process).[132] There is strong evidence that the laws of black hole mechanics are, in fact, a subset of the laws of thermodynamics, and that the black hole area is proportional to its entropy.[133] This leads to a modification of the original laws of black hole mechanics: for instance, as the second law of black hole mechanics becomes part of the second law of thermodynamics, it is possible for black hole area to decrease—as long as other processes ensure that, overall, entropy increases. As thermodynamical objects with non-zero temperature, black holes should emit thermal radiation. Semi-classical calculations indicate that indeed they do, with the surface gravity playing the role of temperature in Planck's law. This radiation is known as Hawking radiation (cf. the quantum theory section, below).[134]
There are other types of horizons. In an expanding universe, an observer may find that some regions of the past cannot be observed ("particle horizon"), and some regions of the future cannot be influenced (event horizon).[135] Even in flat Minkowski space, when described by an accelerated observer (Rindler space), there will be horizons associated with a semi-classical radiation known as Unruh radiation.[136]
Singularities
Another general—and quite disturbing—feature of general relativity is the appearance of spacetime boundaries known as singularities. Spacetime can be explored by following up on timelike and lightlike geodesics—all possible ways that light and particles in free fall can travel. But some solutions of Einstein's equations have "ragged edges"—regions known as spacetime singularities, where the paths of light and falling particles come to an abrupt end, and geometry becomes ill-defined. In the more interesting cases, these are "curvature singularities", where geometrical quantities characterizing spacetime curvature, such the Ricci scalar, take on infinite values.[137] Well-known examples of spacetimes with future singularities—where worldlines end—are the Schwarzschild solution, which describes a singularity inside an eternal static black hole,[138] or the Kerr solution with its ring-shaped singularity inside an eternal rotating black hole.[139] The Friedmann-Lemaître-Robertson-Walker solutions, and other spacetimes describing universes, have past singularities on which worldlines begin, namely big bang singularities, and some have future singularities (big crunch) as well.[140]
Given that these examples are all highly symmetric—and thus simplified—it is tempting to conclude that the occurrence of singularities is an artefact of idealization. The famous singularity theorems, proved using the methods of global geometry, say otherwise: singularities are a generic feature of general relativity, and unavoidable once the collapse of an object with realistic matter properties has proceeded beyond a certain stage[141] and also at the beginning of a wide class of expanding universes.[142] However, the theorems say little about the properties of singularities, and much of current research is devoted to characterizing these entities' generic structure (hypothesized e.g. by the so-called BKL conjecture).[143] The cosmic censorship hypothesis states that all realistic future singularities (no perfect symmetries, matter with realistic properties) are safely hidden away behind a horizon, and thus invisible to all distant observers. While no formal proof yet exists, numerical simulations offer supporting evidence of its validity.[144]
Evolution equations
Each solution of Einstein's equation encompasses the whole history of a universe—it is not just some snapshot of how things are, but a whole, possibly matter-filled, spacetime. It describes the state of matter and geometry everywhere and at every moment in that particular universe. By this token, Einstein's theory appears to be different from most other physical theories, which specify evolution equations for physical systems: if the system is in a given state at some given moment, the laws of physics allow extrapolation into the past or future. Further differences between Einsteinian gravity and other fields are that the former is self-interacting (that is, non-linear even in the absence of other fields), and that it has no fixed background structure—the stage itself evolves as the cosmic drama is played out.[145]
To understand Einstein's equations as partial differential equations, it is helpful to formulate them in a way that describes the evolution of the universe over time. This is done in so-called "3+1" formulations, where spacetime is split into three space dimensions and one time dimension. The best-known example is the ADM formalism.[146] These decompositions show that the spacetime evolution equations of general relativity are well-behaved: solutions always exist, and are uniquely defined, once suitable initial conditions have been specified.[147] Such formulations of Einstein's field equations are the basis of numerical relativity.[148]
Global and quasi-local quantities
The notion of evolution equations is intimately tied in with another aspect of general relativistic physics. In Einstein's theory, it turns out to be impossible to find a general definition for a seemingly simple property such as a system's total mass (or energy). The main reason is that the gravitational field—like any physical field—must be ascribed a certain energy, but that it proves to be fundamentally impossible to localize that energy.[149]
Nevertheless, there are possibilities to define a system's total mass, either using a hypothetical "infinitely distant observer" (ADM mass)[150] or suitable symmetries (Komar mass).[151] If one excludes from the system's total mass the energy being carried away to infinity by gravitational waves, the result is the so-called Bondi mass at null infinity.[152] Just as in classical physics, it can be shown that these masses are positive.[153] Corresponding global definitions exist for momentum and angular momentum.[154] There have also been a number of attempts to define quasi-local quantities, such as the mass of an isolated system formulated using only quantities defined within a finite region of space containing that system. The hope is to obtain a quantity useful for general statements about isolated systems, such as a more precise formulation of the hoop conjecture.[155]
Relationship with quantum theory
If general relativity is considered one of the two pillars of modern physics, quantum theory, the basis of our understanding of matter from elementary particles to solid state physics, is the other.[156] However, it is still an open question of how the concepts of quantum theory can be reconciled with those of general relativity.
Quantum field theory in curved spacetime
Ordinary quantum field theories, which form the basis of modern elementary particle physics, are defined in flat Minkowski space, which is an excellent approximation when it comes to describing the behavior of microscopic particles in weak gravitational fields like those found on Earth.[157] In order to describe situations in which gravity is strong enough to influence (quantum) matter, yet not strong enough to require quantization itself, physicists have formulated quantum field theories in curved spacetime. These theories rely on classical general relativity to describe a curved background spacetime, and define a generalized quantum field theory to describe the behavior of quantum matter within that spacetime.[158] Using this formalism, it can be shown that black holes emit a blackbody spectrum of particles known as Hawking radiation, leading to the possibility that they evaporate over time.[159] As briefly mentioned above, this radiation plays an important role for the thermodynamics of black holes.[160]
Quantum gravity
- See also: String theory and Loop quantum gravity
The demand for consistency between a quantum description of matter and a geometric description of spacetime,[161] as well as the appearance of singularities (where curvature length scales become microscopic), indicate the need for a full theory of quantum gravity: for an adequate description of the interior of black holes, and of the very early universe, a theory is required in which gravity and the associated geometry of spacetime are described in the language of quantum physics.[162] Despite major efforts, no complete and consistent theory of quantum gravity is currently known, even though a number of promising candidates exists.[163]

Attempts to generalize ordinary quantum field theories, used in elementary particle physics to describe fundamental interactions, so as to include gravity have led to serious problems. At low energies, this approach proves successful, in that it results in an acceptable effective (quantum) field theory of gravity.[164] At very high energies, however, the result are models devoid of all predictive power ("non-renormalizability").[165]
One attempt to overcome these limitations is string theory, a quantum theory not of point particles, but of minute one-dimensional extended objects.[166] The theory promises to be a unified description of all particles and interactions, including gravity;[167] the price to pay are unusual features such as six extra dimensions of space in addition to the usual three.[168] In what is called the second superstring revolution, it was conjectured that both string theory and a unification of general relativity and supersymmetry known as supergravity[169] form part of a hypothesized eleven-dimensional model known as M-theory, which would constitute a uniquely defined and consistent theory of quantum gravity.[170]
Another approach starts with the canonical quantization procedures of quantum theory. Using the initial-value-formulation of general relativity (cf. the section on evolution equations, above), the result is the Wheeler-deWitt equation (an analogue of the Schrödinger equation) which, regrettably, turns out to be ill-defined.[171] However, with the introduction of what are now known as Ashtekar variables,[172] this leads to a promising model known as loop quantum gravity. Space is represented by a web-like structure called a spin network, evolving over time in discrete steps.[173]
Depending on which features of general relativity and quantum theory are accepted unchanged, and on what level changes are introduced,[174] there are numerous other attempts to arrive at a viable theory of quantum gravity, some examples being dynamical triangulations,[175] causal sets,[176] twistor models[177] or the path-integral based models of quantum cosmology.[178]
All candidate theories still have major formal and conceptual problems to overcome. They also face the common problem that, as yet, there is no way to put quantum gravity predictions to experimental tests (and thus to decide between the candidates where their predictions vary), although there is hope for this to change as future data from cosmological observations and particle physics experiments becomes available.[179]
Current status
General relativity has emerged as a highly successful model of gravitation and cosmology, which has so far passed every unambiguous observational and experimental test. Even so, there are strong indications the theory is incomplete.[180] The problem of quantum gravity and the question of the reality of spacetime singularities remain open.[181] Observational data that is taken as evidence for dark energy and dark matter could indicate the need for new physics,[182] and while the so-called Pioneer anomaly might yet admit of a conventional explanation, it, too, could be a harbinger of new physics.[183] Even taken as is, general relativity is rich with possibilities for further exploration. Mathematical relativists seek to understand the nature of singularities and the fundamental properties of Einstein's equations,[184] and increasingly powerful computer simulations (such as those describing merging black holes) are run.[185] The race for the first direct detection of gravitational waves continues apace,[186] in the hope of creating opportunities to test the theory's validity for much stronger gravitational fields than has been possible to date.[187] More than ninety years after its publication, general relativity remains a highly active area of research.[188]



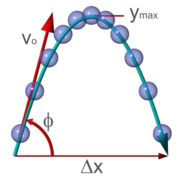






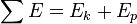

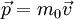
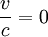
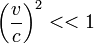
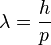




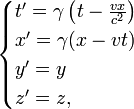



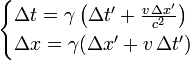

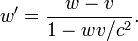






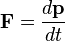





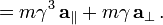



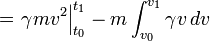







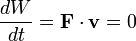













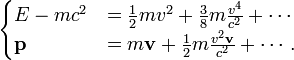
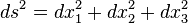
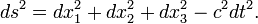







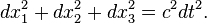
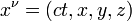





![T^{\left[i_1',i_2',\dots,i_p'\right]}_{\left[j_1',j_2',\dots,j_q'\right]} = \Lambda^{i_1'}{}_{i_1}\Lambda^{i_2'}{}_{i_2}\cdots\Lambda^{i_p'}{}_{i_p} \Lambda_{j_1'}{}^{j_1}\Lambda_{j_2'}{}^{j_2}\cdots\Lambda_{j_q'}{}^{j_q} T^{\left[i_1,i_2,\dots,i_p\right]}_{\left[j_1,j_2,\dots,j_q\right]}](http://upload.wikimedia.org/math/5/f/1/5f10063892eef437b2a03d2a0fa9d05d.png)


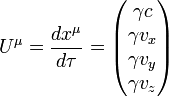
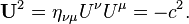









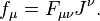
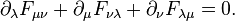










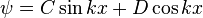 (
(





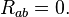






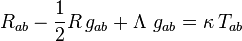

No comments:
Post a Comment