Nuclear Structure

An atom consists of an extremely small, positively charged nucleus surrounded by a cloud of negatively charged electrons. Although typically the nucleus is less than one ten-thousandth the size of the atom, the nucleus contains more than 99.9% of the mass of the atom! Nuclei consist of positively charged protons and electrically neutral neutrons held together by the so-called strong or nuclear force. This force is much stronger than the familiar electrostatic force that binds the electrons to the nucleus, but its range is limited to distances on the order of a few x10-15 meters.
The number of protons in the nucleus, Z, is called the atomic number. This determines what chemical element the atom is. The number of neutrons in the nucleus is denoted by N. The atomic mass of the nucleus, A, is equal to Z + N. A given element can have many different isotopes, which differ from one another by the number of neutrons contained in the nuclei. In a neutral atom, the number of electrons orbiting the nucleus equals the number of protons in the nucleus. Since the electric charges of the proton and the electron are +1 and -1 respectively (in units of the proton charge), the net charge of the atom is zero. At present, there are 112 known elements which range from the lightest, hydrogen, to the recently discovered and yet to-be-named element 112. All of the elements heavier than uranium are man made. Among the elements are approximately 270 stable isotopes, and more than 2000 unstable isotopes.
Radioactivity
In 1896, Henri Becquerel was working with compounds containing the element uranium. To his surprise, he found that photographic plates covered to keep out light became fogged, or partially exposed, when these uranium compounds were anywhere near the plates. This fogging suggested that some kind of ray had passed through the plate coverings. Several materials other than uranium were also found to emit these penetrating rays. Materials that emit this kind of radiation are said to be radioactive and to undergo radioactive decay.
In 1899, Ernest Rutherford discovered that uranium compounds produce three different kinds of radiation. He separated the radiations according to their penetrating abilities and named them a alpha, b beta, and g gamma radiation, after the first three letters of the Greek alphabet. The a radiation can be stopped by a sheet of paper. Rutherford later showed that an alpha particle is the nucleus of a He atom, 4He. Beta particles were later identified as high speed electrons. Six millimeters of aluminum are needed to stop most b particles. Several millimeters of lead are needed to stop g rays , which proved to be high energy photons. Alpha particles and g rays are emitted with a specific energy that depends on the radioactive isotope. Beta particles, however, are emitted with a continuous range of energies from zero up to the maximum allowed for by the particular isotope.
α decay
The emission of an a particle, or 4He nucleus, is a process called a decay. Since a particles contain protons and neutrons, they must come from the nucleus of an atom. The nucleus that results from a decay will have a mass and charge different from those of the original nucleus. A change in nuclear charge means that the element has been changed into a different element. Only through such radioactive decays or nuclear reactions can transmutation, the age-old dream of the alchemists, actually occur. The mass number, A, of an a particle is four, so the mass number, A, of the decaying nucleus is reduced by four. The atomic number, Z, of 4He is two, and therefore the atomic number of the nucleus, the number of protons, is reduced by two. This can be written as an equation analogous to a chemical reaction. For example, for the decay of an isotope of the element seaborgium, 263Sg:
| |
The atomic number of the nucleus changes from 106 to 104, giving rutherfordium an atomic mass of 263-4=259. a decay typically occurs in heavy nuclei where the electrostatic repulsion between the protons in the nucleus is large. Energy is released in the process of a decay. Careful measurements show that the sum of the masses of the daughter nucleus and the a particle is a bit less than the mass of the parent isotope. Einstein's famous equation, E=mc2, which says that mass is proportional to energy, explains this fact by saying that the mass that is lost in such decay is converted into the kinetic energy carried away by the decay products.
β Decay
Beta particles are negatively charged electrons emitted by the nucleus. Since the mass of an electron is a tiny fraction of an atomic mass unit, the mass of a nucleus that undergoes b decay is changed by only a tiny amount. The mass number is unchanged. The nucleus contains no electrons. Rather, b decay occurs when a neutron is changed into a proton within the nucleus. An unseen neutrino,![]() , accompanies each b decay. The number of protons, and thus the atomic number, is increased by one. For example, the isotope 14C is unstable and emits a β particle, becoming the stable isotope 14N:
, accompanies each b decay. The number of protons, and thus the atomic number, is increased by one. For example, the isotope 14C is unstable and emits a β particle, becoming the stable isotope 14N:
| |
In a stable nucleus, the neutron does not decay. A free neutron, or one bound in a nucleus that has an excess of neutrons, can decay by emitting a b particle. Sharing the energy with the b particle is a neutrino. The neutrino has little or no mass and is uncharged, but, like the photon, it carries momentum and energy. The source of the energy released in b decay is explained by the fact that the mass of the parent isotope is larger than the sum of the masses of the decay products. Mass is converted into energy just as Einstein predicted.
γ Decay
Gamma rays are a type of electromagnetic radiation that results from a redistribution of electric charge within a nucleus. A g ray is a high energy photon. The only thing which distinguishes a g ray from the visible photons emitted by a light bulb is its wavelength; the g ray's wavelength is much shorter. For complex nuclei there are many different possible ways in which the neutrons and protons can be arranged within the nucleus. Gamma rays can be emitted when a nucleus undergoes a transition from one such configuration to another. For example, this can occur when the shape of the nucleus undergoes a change. Neither the mass number nor the atomic number is changed when a nucleus emits a g ray in the reaction
The time required for half of the atoms in any given quantity of a radioactive isotope to decay is the half-life of that isotope. Each particular isotope has its own half-life. For example, the half-life of 238U is 4.5 billion years. That is, in 4.5 billion years, half of the 238U on Earth will have decayed into other elements. In another 4.5 billion years, half of the remaining 238U will have decayed. One fourth of the original material will remain on Earth after 9 billion years. The half-life of 14C is 5730 years, thus it is useful for dating archaeological material. Nuclear half-lives range from tiny fractions of a second to many, many times the age of the universe.
For more information on half-life and isotopes, please refer to the Isotopes Project at LBNL where you can also find the Table of Isotopes online.
Reactions
If nuclei come close enough together, they can interact with one another through the strong nuclear force, and reactions between the nuclei can occur. As in chemical reactions, nuclear reactions can either be exothermic (i.e. release energy) or endothermic (i.e. require energy input). Two major classes of nuclear reactions are of importance: fusion and fission.
Nuclear Reactions
In nuclear physics, a nuclear reaction is the process in which two nuclei or nuclear particles collide to produce products different from the initial particles. In principle a reaction can involve more than two particles colliding, but because the probability of three or more nuclei to meet at the same time at the same place is much less than for two nuclei, such an event is exceptionally rare. While the transformation is spontaneous in the case of radioactive decay, it is initiated by a particle in the case of a nuclear reaction. If the particles collide and separate without changing, the process is called an elastic collision rather than a reaction.
In the symbolic figure shown to the right, 63Li and deuterium react to form the highly excited intermediate nucleus 84Be which then decays immediately into two alpha particles. Protons are symbolically represented by red spheres, and neutrons by blue spheres.
To make the sums correct, the second nucleus to the right must have atomic number 2 and mass number 4; it is therefore also Helium-4. The complete equation therefore reads:
or more simply:
| 63Li | + | 21H | → | 2 42He |
Notation
Instead of using the full equations as shown in the previous section, in many situations a compact notation is used to describe nuclear reactions. This is A(b,c)D, which is equivalent to A + b gives c + D. Common light particles are often abbreviated in this shorthand, typically p for proton, n for neutron, α representing an alpha particle or Helium-4, etc. The reaction above would be written as Li-6(d,α)α.[1][2]
Energy conservation
Kinetic energy may be released during the course of a reaction (exothermic reaction) or kinetic energy may have to be supplied for the reaction to take place (endothermic reaction). This can be calculated by reference to a table of very accurate particle rest masses (see http://physics.nist.gov/PhysRefData/Compositions/index.html), as follows. According to the reference tables, the 63Li nucleus has a relative atomic mass of 6.015 atomic mass units (abbreviated u), the deuteron has 2.014 u, and the helium-4 nucleus has 4.0026 u Thus:
- Total rest mass on left side = 6.015 + 2.014 = 8.029 u
- Total rest mass on right side = 2 × 4.0026 = 8.0052 u
- Missing rest mass = 8.029 - 8.0052 = 0.0238 atomic mass units.
In a nuclear reaction, the total (relativistic) energy is conserved. The "missing" rest mass must therefore reappear as kinetic energy released in the reaction; its source is the nuclear binding energy. Using Einstein's mass-energy equivalence formula E = mc², the amount of energy released can be determined. We first need the energy equivalent of one atomic mass unit:
- 1 u c2 = (1.66054 × 10-27 kg) × (2.99792 × 108 m/s)2
- = 1.49242 × 10-10 kg (m/s)2 = 1.49242 × 10-10 J (Joule)
- × (1 MeV / 1.60218 × 10-13 J)
- = 931.49 MeV,
- so 1 u c2 = 931.49 MeV.
Hence, the energy released is 0.0238 × 931 MeV = 22.4 MeV.
Expressed differently: the mass is reduced by 0.3 %, corresponding to 0.3 % of 90 PJ/kg is 300 TJ/kg.
This is a large amount of energy for a nuclear reaction; the amount is so high because the binding energy per nucleon of the helium-4 nucleus is unusually high, because the He-4 nucleus is doubly magic. (The He-4 nucleus is unusually stable and tightly-bound for the same reason that the helium atom is inert: each pair of protons and neutrons in He-4 occupies a filled 1s nuclear orbital in the same way that the pair of electrons in the helium atom occupy a filled 1s electron orbital). Husking corn is an example of a nuclear reaction. Consequently, alpha particles appear frequently on the right hand side of nuclear reactions.
The energy released in a nuclear reaction can appear mainly in one of three ways:
- kinetic energy of the product particles
- emission of very high energy photons, called gamma rays
- some energy may remain in the nucleus, as a metastable energy level.
When the product nucleus is metastable, this is indicated by placing an asterisk ("*") next to its atomic number. This energy is eventually released through nuclear decay.
A small amount of energy may also emerge in the form of X-rays. Generally, the product nucleus has a different atomic number, and thus the configuration of its electron shells is wrong. As the electrons rearrange themselves and drop to lower energy levels, internal transition X-rays (X-rays with precisely defined emission lines) may be emitted.
Q-value and energy balance
In writing down the reaction equation, in a way analogous to a chemical equation, one may in addition give the reaction energy on the right side:
-
- Target nucleus + projectile -> Final nucleus + ejectile + Q.
For the particular case discussed above, the reaction energy has already been calculated as Q = 22.4 MeV. Hence:
The reaction energy (the "Q-value") is positive for exothermal reactions and negative for endothermal reactions. On the one hand, it is the difference between the sums of kinetic energies on the final side and on the initial side. But on the other hand, it is also the difference between the nuclear rest masses on the initial side and on the final side (in this way, we have calculated the Q-value above).
Reaction rates
If the reaction equation is balanced, that does not mean that the reaction really occurs. The rate at which reactions occur depends on the particle energy, the particle flux and the reaction cross section.
[edit] Neutrons vs ions
In the initial collision which begins the reaction, the particles must approach closely enough so that the short range strong force can affect them. As most common nuclear particles are positively charged, this means they must overcome considerable electrostatic repulsion before the reaction can begin. Even if the target nucleus is part of a neutral atom, the other particle must penetrate well beyond the electron cloud and closely approach the nucleus, which is positively charged. Thus, such particles must be first accelerated to high energy, for example by:
- particle accelerators
- nuclear decay (alpha particles are the main type of interest here, since beta and gamma rays are rarely involved in nuclear reactions)
- very high temperatures, on the order of millions of degrees, producing thermonuclear reactions
- cosmic rays
Also, since the force of repulsion is proportional to the product of the two charges, reactions between heavy nuclei are rarer, and require higher initiating energy, than those between a heavy and light nucleus; while reactions between two light nuclei are the most common ones.
Neutrons, on the other hand, have no electric charge to cause repulsion, and are able to effect a nuclear reaction at very low energies. In fact at extremely low particle energies (corresponding, say, to thermal equilibrium at room temperature), the neutron's de Broglie wavelength is greatly increased, possibly greatly increasing its capture cross section, at energies close to resonances of the nuclei involved. Thus low energy neutrons may be even more reactive than high energy neutrons.
Notable types
While the number of possible nuclear reactions is immense, there are several types which are more common, or otherwise notable. Some examples include:
- Fusion reactions - two light nuclei join to form a heavier one, with additional particles (usually protons or neutrons) thrown off to conserve momentum.
- Fission reactions - a very heavy nucleus, spontaneously or after absorbing additional light particles (usually neutrons), splits into two or sometimes three pieces. (α decay is not usually called fission.)
- Spallation - a nucleus is hit by a particle with sufficient energy and momentum to knock out several small fragments or, smash it into many fragments.
- Induced gamma emission belongs to a class in which only photons were involved in creating and destroying states of nuclear excitation.
[edit] Direct reactions
An intermediate energy projectile transfers energy or picks up or loses nucleons to the nucleus in a single quick (10−21 second) event. Energy and momentum transfer are relatively small. These are particularly useful in experimental nuclear physics, because the reaction mechanisms are often simple enough to calculate with sufficient accuracy to probe the structure of the target nucleus.
Inelastic scattering
Only energy and momentum are transferred.
- (p,p') tests differenced between nuclear states
- (α,α') measures nuclear surface shapes and sized. Since α particles that hit the nucleus react more violently, elastic and shallow inelastic α scattering are sensitive to the shapes and sizes of the targets, like light scattered from a small black object.
- (e,e') is useful for probing the interior structure. Since electrons interact less strongly than do protons and neutrons, they reach to the centers of the targets and their wave functions are less distorted by passing through the nucleus.
Transfer reactions
Usually at moderately low energy, one or more nucleons are transferred between the projectile and target. These are useful in studying outer shell structure of nuclei.
- (α,n) and (α,p) reactions. Some of the earliest nuclear reactions studied involved an alpha particle produced by alpha decay, knocking a nucleon from a target nucleus.
- (d,n) and (d,p) reactions. A deuteron beam impinges on a target; the target nuclei absorb either the neutron or proton from the deuteron. The deuteron is so loosely bound that this is almost the same as proton or neutron capture. A compound nucleus may be formed, leading to additional neutrons being emitted more slowly. (d,n) reactions are used to generate energetic neutrons.
- The strangeness exchange reaction (K,π) has been used to study hypernuclei.
Reactions with neutrons are important in nuclear reactors and nuclear weapons. While the best known neutron reactions are neutron scattering, neutron capture, and nuclear fission, for some light nuclei, the most probable reaction with a thermal neutron is a transfer reaction:
| (n,α) | 6Li + n → T + α | 10B + n → 7Li + α | 17O + n → 14C + α | 21Ne + n → 18O + α | 37Ar + n → 34S + α |
| (n,p) | 3He + n → T + p | 7Be + n → 7Li + p | 14N + n → 14C + p | 22Na + n → 22Ne + p |
|
Some reactions are only possible with fast neutrons:
- (n,2n) reactions produce small amounts of protactinium-231 and uranium-232 in the thorium cycle which is otherwise relatively free of highly radioactive actinide products.
- 9Be + n → 2α + 2n can contribute some additional neutrons in the beryllium neutron reflector of a nuclear weapon.
- 7Li + n → T + α + n unexpectedly contributed additional yield in Castle Bravo, Castle Romeo, and Castle Yankee, the three highest-yield nuclear tests conducted by the United States.
Compound nuclear reactions
Either a low energy projectile is absorbed or a higher energy particle transfers energy to the nucleus, leaving it with too much energy to be fully bound together. On a time scale of about 10−19 seconds, particles, usually neutrons, are "boiled" off. That is, it remains together until enough energy happens to be concentrated in one neutron to escape the mutual attraction. Charged particles rarely boil off because of the coulomb barrier. The excited quasi-bound nucleus is called a compound nucleus.
- Low energy (e, e' xn), (γ, xn) (the xn indicating one or more neutrons), where the gamma or virtual gamma energy is near the Giant dipole resonance These increase the need for radiation shielding around electron accelerators
- Further information: Spallation#Nuclear spallation
Calculation
Applying the methods of scattering by two potentials, the plane wave of each free charged particle is replaced by the exact solution for a charged particle moving in the presence of another point charge.
Direct nuclear reactions are most often calculated by some form of distorted wave Born approximation. Applying again scattering by two potentials, the coulomb solutions and neutron plane waves are replaced by the optical model wave functions for the incident and outgoing particles moving in and near the nucleus. These are obtained mostly from elastic scattering experiments, and from inelastic scattering to vibrational and rotational collective excitations. The reaction itself is then modeled by the Born approximation. That is, the excitation or transfer process is treated as a first order perturbation on elastic scattering. An early improvement on this was to exactly treat the coupling between a small number of excited states, known as coupled channels Born approximation.
In nuclear physics and nuclear chemistry, nuclear fusion is the process by which multiple like-charged atomic nuclei join together to form a heavier nucleus. It is accompanied by the release or absorption of energy. Iron and nickel nuclei have the largest binding energies per nucleon of all nuclei. The fusion of two nuclei with lower mass than iron generally releases energy while the fusion of nuclei heavier than iron absorbs energy; vice-versa for the reverse process, nuclear fission.
Nuclear fusion occurs naturally in stars. Artificial fusion in human enterprises has also been achieved, although not yet completely controlled. Building upon the nuclear transmutation experiments of Ernest Rutherford done a few years earlier, fusion of light nuclei (hydrogen isotopes) was first observed by Mark Oliphant in 1932, and the steps of the main cycle of nuclear fusion in stars were subsequently worked out by Hans Bethe throughout the remainder of that decade. Research into fusion for military purposes began in the early 1940s, as part of the Manhattan Project, but was not successful until 1952. Research into controlled fusion for civilian purposes began in the 1950s, and continues to this day.
Fusion reactions power the stars and produce all but the lightest elements in a process called nucleosynthesis. While the fusion of lighter elements in stars releases energy, production of the heavier elements absorbs energy.
When the fusion reaction is a sustained uncontrolled chain, it can result in a thermonuclear explosion, such as that generated by a hydrogen bomb. Reactions which are not self-sustaining can still release considerable energy, as well as large numbers of neutrons.
Research into controlled fusion, with the aim of producing fusion power for the production of electricity, has been conducted for over 50 years. It has been accompanied by extreme scientific and technological difficulties, but resulted in steady progress. As of the present, break-even (self-sustaining) controlled fusion reaction have been demonstrated in a few tokamak-type reactors around the world and resulted in producing workable design of the reactor which will deliver ten times more fusion energy than the amount of energy needed to heat up its plasma to required temperatures (see ITER which is scheduled to be operational in 2018).
It takes considerable energy to force nuclei to fuse, even those of the lightest element, hydrogen. This is because all nuclei have a positive charge (due to their protons), and as like charges repel, nuclei strongly resist being put too close together. Accelerated to high speeds (that is, heated to thermonuclear temperatures), they can overcome this electromagnetic repulsion and get close enough for the attractive nuclear force to be sufficiently strong to achieve fusion. The fusion of lighter nuclei, creating a heavier nucleus and a free neutron, will generally release more energy than it took to force them together-an exothermic process that can produce self-sustaining reactions.
The energy released in most nuclear reactions is much larger than that in chemical reactions, because the binding energy that holds a nucleus together is far greater than the energy that holds electrons to a nucleus. For example, the ionization energy gained by adding an electron to a hydrogen nucleus is 13.6 electron volts - less than one-millionth of the 17 MeV released in the D-T (deuterium-tritium) reaction shown to the top right. Fusion reactions have an energy density many times greater than nuclear fission —- i.e., per unit of mass the reactions produce far greater energies, even though individual fission reactions are generally much more energetic than individual fusion reactions-which are themselves millions of times more energetic than chemical reactions. Only the direct conversion of mass into energy, such as with collision of matter and antimatter, is more energetic per unit of mass than nuclear fusion.
Requirements
A substantial energy barrier of electrostatic forces must be overcome before fusion can occur. At large distances two naked nuclei repel one another because of the repulsive electrostatic force between their positively charged protons. If two nuclei can be brought close enough together, however, the electrostatic repulsion can be overcome by the attractive nuclear force which is stronger at close distances.
When a nucleon such as a proton or neutron is added to a nucleus, the nuclear force attracts it to other nucleons, but primarily to its immediate neighbours due to the short range of the force. The nucleons in the interior of a nucleus have more neighboring nucleons than those on the surface. Since smaller nuclei have a larger surface area-to-volume ratio, the binding energy per nucleon due to the strong force generally increases with the size of the nucleus but approaches a limiting value corresponding to that of a fully surrounded nucleon.
The electrostatic force, on the other hand, is an inverse-square force, so a proton added to a nucleus will feel an electrostatic repulsion from all the other protons in the nucleus. The electrostatic energy per nucleon due to the electrostatic force thus increases without limit as nuclei get larger.
The net result of these opposing forces is that the binding energy per nucleon generally increases with increasing size, up to the elements iron and nickel, and then decreases for heavier nuclei. Eventually, the binding energy becomes negative and very heavy nuclei are not stable. The four most tightly bound nuclei, in decreasing order of binding energy, are 62Ni, 58Fe, 56Fe, and 60Ni.[1] Even though the nickel isotope ,62Ni, is more stable, the iron isotope 56Fe is an order of magnitude more common. This is due to a greater disintegration rate for 62Ni in the interior of stars driven by photon absorption.
A notable exception to this general trend is the helium-4 nucleus, whose binding energy is higher than that of lithium, the next heavier element. The Pauli exclusion principle provides an explanation for this exceptional behavior—it says that because protons and neutrons are fermions, they cannot exist in exactly the same state. Each proton or neutron energy state in a nucleus can accommodate both a spin up particle and a spin down particle. Helium-4 has an anomalously large binding energy because its nucleus consists of two protons and two neutrons; so all four of its nucleons can be in the ground state. Any additional nucleons would have to go into higher energy states.
The situation is similar if two nuclei are brought together. As they approach each other, all the protons in one nucleus repel all the protons in the other. Not until the two nuclei actually come in contact can the strong nuclear force take over. Consequently, even when the final energy state is lower, there is a large energy barrier that must first be overcome. It is called the Coulomb barrier.
The Coulomb barrier is smallest for isotopes of hydrogen—they contain only a single positive charge in the nucleus. A bi-proton is not stable, so neutrons must also be involved, ideally in such a way that a helium nucleus, with its extremely tight binding, is one of the products.
Using deuterium-tritium fuel, the resulting energy barrier is about 0.01 MeV.[citation needed] In comparison, the energy needed to remove an electron from hydrogen is 13.6 eV, about 750 times less energy. The (intermediate) result of the fusion is an unstable 5He nucleus, which immediately ejects a neutron with 14.1 MeV.[citation needed] The recoil energy of the remaining 4He nucleus is 3.5 MeV,[citation needed] so the total energy liberated is 17.6 MeV.[citation needed] This is many times more than what was needed to overcome the energy barrier.
If the energy to initiate the reaction comes from accelerating one of the nuclei, the process is called beam-target fusion; if both nuclei are accelerated, it is beam-beam fusion. If the nuclei are part of a plasma near thermal equilibrium, one speaks of thermonuclear fusion. Temperature is a measure of the average kinetic energy of particles, so by heating the nuclei they will gain energy and eventually have enough to overcome this 0.01 MeV. Converting the units between electronvolts and kelvins shows that the barrier would be overcome at a temperature in excess of 120 million kelvins, obviously a very high temperature.
There are two effects that lower the actual temperature needed. One is the fact that temperature is the average kinetic energy, implying that some nuclei at this temperature would actually have much higher energy than 0.01 MeV, while others would be much lower. It is the nuclei in the high-energy tail of the velocity distribution that account for most of the fusion reactions. The other effect is quantum tunneling. The nuclei do not actually have to have enough energy to overcome the Coulomb barrier completely. If they have nearly enough energy, they can tunnel through the remaining barrier. For this reason fuel at lower temperatures will still undergo fusion events, at a lower rate.
The reaction cross section σ is a measure of the probability of a fusion reaction as a function of the relative velocity of the two reactant nuclei. If the reactants have a distribution of velocities, e.g. a thermal distribution with thermonuclear fusion, then it is useful to perform an average over the distributions of the product of cross section and velocity. The reaction rate (fusions per volume per time) is <σv> times the product of the reactant number densities:
![]()
If a species of nuclei is reacting with itself, such as the DD reaction, then the product n1n2 must be replaced by (1 / 2)n2.
![]() increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of 10 – 100 keV. At these temperatures, well above typical ionization energies (13.6 eV in the hydrogen case), the fusion reactants exist in a plasma state.
increases from virtually zero at room temperatures up to meaningful magnitudes at temperatures of 10 – 100 keV. At these temperatures, well above typical ionization energies (13.6 eV in the hydrogen case), the fusion reactants exist in a plasma state.
The significance of <σv> as a function of temperature in a device with a particular energy confinement time is found by considering the Lawson criterion.
One force capable of confining the fuel well enough to satisfy the Lawson criterion is gravity. The mass needed, however, is so great that gravitational confinement is only found in stars (the smallest of which are brown dwarfs). Even if the more reactive fuel deuterium were used, a mass greater than that of the planet Jupiter would be needed.
The charged ions of fusion fuel and magnetic field lines (see Guiding center#Gyration), and the fuel is therefore trapped along the field lines. A variety of magnetic configurations exist, including the toroidal geometries of tokamaks and stellarators and open ended mirror confinement systems.
A third confinement principle is to apply a rapid pulse of energy to a large part of the surface of a pellet of fusion fuel, causing it to simultaneously "implode" and heat to very high pressure and temperature. If the fuel is dense enough and hot enough, the fusion reaction rate will be high enough to burn a significant fraction of the fuel before it has dissipated. To achieve these extreme conditions, the initially cold fuel must be explosively compressed. Inertial confinement is used in the hydrogen bomb, where the driver is x-rays created by a fission bomb. Inertial confinement is also attempted in "controlled" nuclear fusion, where the driver is a laser, ion, or electron beam, or a Z-pinch. Another method is to use conventional high explosive material to compress a fuel to fusion conditions.The UTIAS explosive-driven-implosion facility was used to produce stable, centered and focused hemispherical implosions to generate neutrons from D-D reactions.The simplest and most direct method proved to be in a predetonated stoichiometric mixture of deuterium-oxygen.The other successful method was using a miniature Voitenko-type compressor[2],where a plane diaphragm was driven by the implosion wave into a secondary small spherical cavity that contained pure deuterium gas at one atmosphere.[3]
Some confinement principles have been investigated, such as muon-catalyzed fusion, the Farnsworth-Hirsch fusor and Polywell (inertial electrostatic confinement), and bubble fusion.
A variety of methods are known to effect nuclear fusion. Some are "cold" in the strict sense that no part of the material is hot (except for the reaction products), some are "cold" in the limited sense that the bulk of the material is at a relatively low temperature and pressure but the reactants are not, and some are "hot" fusion methods that create macroscopic regions of very high temperature and pressure.
- Muon-catalyzed fusion is a well-established and reproducible fusion process that occurs at ordinary temperatures. It was studied in detail by Steven Jones in the early 1980s. It has not been reported to produce net energy. Net energy production from this reaction is not believed to be possible because of the energy required to create muons, their 2.2 µs half-life, and the chance that a muon will bind to the new alpha particle and thus
Generally cold, locally hot fusion
- Accelerator based light-ion fusion. Using particle accelerators it is possible to achieve particle kinetic energies sufficient to induce many light ion fusion reactions. Accelerating light ions is relatively easy, cheap, and can be done in an efficient manner - all it takes is a vacuum tube, a pair of electrodes, and a high-voltage transformer; fusion can be observed with as little as 10 kilovolt between electrodes. The key problem with accelerator-based fusion (and with cold targets in general) is that fusion cross sections are many orders of magnitude lower than Coulomb interaction cross sections. Therefore vast majority of ions ends up expending their energy on bremsstrahlung and ionization of atoms of the target. Devices referred to as sealed-tube neutron generators are particularly relevant to this discussion. These small devices are miniature particle accelerators filled with deuterium and tritium gas in an arrangement which allows ions of these nuclei to be accelerated against hydride targets, also containing deuterium and tritium, where fusion takes place. Hundreds of neutron generators are produced annually for use in the petroleum industry where they are used in measurement equipment for locating and mapping oil reserves. Despite periodic reports in the popular press by scientists claiming to have invented "table-top" fusion machines, neutron generators have been around for half a century. The sizes of these devices vary but the smallest instruments are often packaged in sizes smaller than a loaf of bread. These devices do not produce a net power output.
- In sonoluminescence, acoustic shock waves create temporary bubbles that collapse shortly after creation, producing very high temperatures and pressures. In 2002, Rusi P. Taleyarkhan reported the possibility that bubble fusion occurs in those collapsing bubbles (aka sonofusion). As of 2005, experiments to determine whether fusion is occurring give conflicting results. If fusion is occurring, it is because the local temperature and pressure are sufficiently high to produce hot fusion.[4] In an episode of Horizon, on BBC television, results were presented showing that, although temperatures were reached which could initiate fusion on a large scale, no fusion was occurring, and inaccuracies in the measuring system were the cause of anomalous results.
- The Farnsworth-Hirsch Fusor is a tabletop device in which fusion occurs. This fusion comes from high effective temperatures produced by electrostatic acceleration of ions. The device can be built inexpensively, but it too is unable to produce a net power output.
- Antimatter-initialized fusion uses small amounts of antimatter to trigger a tiny fusion explosion. This has been studied primarily in the context of making nuclear pulse propulsion feasible. This is not near becoming a practical power source, due to the cost of manufacturing antimatter alone.
- Pyroelectric fusion was reported in April 2005 by a team at UCLA. The scientists used a pyroelectric crystal heated from −34 to 7°C (−30 to 45°F), combined with a tungsten needle to produce an electric field of about 25 gigavolts per meter to ionize and accelerate deuterium nuclei into an erbium deuteride target. Though the energy of the deuterium ions generated by the crystal has not been directly measured, the authors used 100 keV (a temperature of about 109 K) as an estimate in their modeling.[5] At these energy levels, two deuterium nuclei can fuse together to produce a helium-3 nucleus, a 2.45 MeV neutron and bremsstrahlung. Although it makes a useful neutron generator, the apparatus is not intended for power generation since it requires far more energy than it produces.[6][7][8][9]
In "standard" "hot" fusion, the fuel reaches tremendous temperature and pressure inside a fusion reactor or nuclear weapon.
The methods in the second group are examples of non-equilibrium systems, in which very high temperatures and pressures are produced in a relatively small region adjacent to material of much lower temperature. In his doctoral thesis for MIT, Todd Rider did a theoretical study of all quasineutral, isotropic, non-equilibrium fusion systems. He demonstrated that all such systems will leak energy at a rapid rate due to bremsstrahlung radiation produced when electrons in the plasma hit other electrons or ions at a cooler temperature and suddenly decelerate. The problem is not as pronounced in a hot plasma because the range of temperatures, and thus the magnitude of the deceleration, is much lower. Note that Rider's work does not apply to non-neutral and/or anisotropic non-equilibrium plasmas.

The most important fusion process in nature is that which powers the stars. The net result is the fusion of four protons into one alpha particle, with the release of two positrons, two neutrinos (which changes two of the protons into neutrons), and energy, but several individual reactions are involved, depending on the mass of the star. For stars the size of the sun or smaller, the proton-proton chain dominates. In heavier stars, the CNO cycle is more important. Both types of processes are responsible for the creation of new elements as part of stellar nucleosynthesis.
At the temperatures and densities in stellar cores the rates of fusion reactions are notoriously slow. For example, at solar core temperature (T ≈ 15 MK) and density (160 g/cm³), the energy release rate is only 276 μW/cm³—about a quarter of the volumetric rate at which a resting human body generates heat.[10] Thus, reproduction of stellar core conditions in a lab for nuclear fusion power production is completely impractical. Because nuclear reaction rates strongly depend on temperature (exp(−E/kT)), then in order to achieve reasonable rates of energy production in terrestrial fusion reactors 10–100 times higher temperatures (compared to stellar interiors) are required T ≈ 0.1–1.0 GK.
Criteria and candidates for terrestrial reactions
In man-made fusion, the primary fuel is not constrained to be protons and higher temperatures can be used, so reactions with larger cross-sections are chosen. This implies a lower Lawson criterion, and therefore less startup effort. Another concern is the production of neutrons, which activate the reactor structure radiologically, but also have the advantages of allowing volumetric extraction of the fusion energy and tritium breeding. Reactions that release no neutrons are referred to as aneutronic.
In order to be useful as a source of energy, a fusion reaction must satisfy several criteria. It must
- be exothermic: This may be obvious, but it limits the reactants to the low Z (number of protons) side of the curve of binding energy. It also makes helium 4He the most common product because of its extraordinarily tight binding, although 3He and 3H also show up;
- involve low Z nuclei: This is because the electrostatic repulsion must be overcome before the nuclei are close enough to fuse;
- have two reactants: At anything less than stellar densities, three body collisions are too improbable. It should be noted that in inertial confinement, both stellar densities and temperatures are exceeded to compensate for the shortcomings of the third parameter of the Lawson criterion, ICF's very short confinement time;
- have two or more products: This allows simultaneous conservation of energy and momentum without relying on the electromagnetic force;
- conserve both protons and neutrons: The cross sections for the weak interaction are too small.
Few reactions meet these criteria. The following are those with the largest cross sections [citation needed]:
| (1) | + | → | ( | 3.5 MeV | ) | + | ( | 14.1 MeV | ) | ||||||||||
| (2i) | + | → | ( | 1.01 MeV | ) | + | ( | 3.02 MeV | ) | | | | | | 50% | ||||
| (2ii) | | | | → | ( | 0.82 MeV | ) | + | ( | 2.45 MeV | ) | | | | | | 50% | ||
| (3) | + | → | ( | 3.6 MeV | ) | + | ( | 14.7 MeV | ) | ||||||||||
| (4) | + | → | | | | + | 2 n0 | | | | | | + | 11.3 MeV | |||||
| (5) | + | → | | | | + | 2 p+ | | | | | | + | 12.9 MeV | |||||
| (6i) | + | → | | | | + | + | | | | + | 12.1 MeV | | 51% | |||||
| (6ii) | | | | → | ( | 4.8 MeV | ) | + | ( | 9.5 MeV | ) | | | | | | 43% | ||
| (6iii) | | | | → | ( | 0.5 MeV | ) | + | ( | 1.9 MeV | ) | + | ( | 11.9 MeV | ) | 6% | |||
| (7i) | + | → | 2 42He | + | 22.4 MeV | ||||||||||||||
| (7ii) | | | | → | + | | + | | | | | | + | 2.56 MeV | |||||
| (7iii) | | | | → | + | | | | | | | | | + | 5.0 MeV | ||||
| (7iv) | | | | → | + | | | | | | | | | + | 3.4 MeV | ||||
| (8) | + | → | ( | 1.7 MeV | ) | + | ( | 2.3 MeV | ) | ||||||||||
| (9) | + | → | 2 42He | + | | | | | | | | | + | 16.9 MeV | |||||
| (10) | + | → | 3 42He | | | | | | | | | | | + | 8.7 MeV |
For reactions with two products, the energy is divided between them in inverse proportion to their masses, as shown. In most reactions with three products, the distribution of energy varies. For reactions that can result in more than one set of products, the branching ratios are given. Some reaction candidates can be eliminated at once.[11]The D-6Li reaction has no advantage compared to p+-115Bbecause it is roughly as difficult to burn but produces substantially more neutrons through 21D-21Dside reactions. There is also a p+-73Lireaction, but the cross section is far too low, except possibly when Ti> 1 MeV, but at such high temperatures an endothermic, direct neutron-producing reaction also becomes very significant. Finally there is also a p+-94Bereaction, which is not only difficult to burn, but 94Becan be easily induced to split into two alpha particles and a neutron. In addition to the fusion reactions, the following reactions with neutrons are important in order to "breed" tritium in "dry" fusion bombs and some proposed fusion reactors:
| + | → | + | ||||||
| + | → | + | + |
To evaluate the usefulness of these reactions, in addition to the reactants, the products, and the energy released, one needs to know something about the cross section. Any given fusion device will have a maximum plasma pressure that it can sustain, and an economical device will always operate near this maximum. Given this pressure, the largest fusion output is obtained when the temperature is chosen so that <σv>/T² is a maximum. This is also the temperature at which the value of the triple product nTτ required for ignition is a minimum, since that required value is inversely proportional to <σv>/T² (see Lawson criterion). (A plasma is "ignited" if the fusion reactions produce enough power to maintain the temperature without external heating.) This optimum temperature and the value of <σv>/T² at that temperature is given for a few of these reactions in the following table.
| fuel | T [keV] | <σv>/T² [m³/s/keV²] |
| 21D-31T | 13.6 | 1.24×10-24 |
| 21D-21D | 15 | 1.28×10-26 |
| 21D-32He | 58 | 2.24×10-26 |
| p+-63Li | 66 | 1.46×10-27 |
| p+-115B | 123 | 3.01×10-27 |
Note that many of the reactions form chains. For instance, a reactor fueled with 31T and 32He will create some 21D, which is then possible to use in the 21D-32He reaction if the energies are "right". An elegant idea is to combine the reactions (8) and (9). The 32He from reaction (8) can react with 63Li in reaction (9) before completely thermalizing. This produces an energetic proton which in turn undergoes reaction (8) before thermalizing. A detailed analysis shows that this idea will not really work well, but it is a good example of a case where the usual assumption of a Maxwellian plasma is not appropriate.
The Proton-Proton Chain
The Proton-Proton Chain is the principal set of reactions for solar-type stars to transform hydrogen to helium:
- 1H + 1H --> 2H + e+ + neutrino
Two protons (p+) react to form Deuterium (2H = 1p+ & 1 n) plus a positron (e+) and a neutrino. In the highly ionized stellar interior the positron will quickly "annihilate" with an electron (e+ + e- --> 2 gamma-rays); the gamma-rays will be absorbed and re-emitted by the dense matter in the stellar interior, gradually diffusing outward and being "degraded" into photons of lower energy. When the gamma-ray energy reaches the photosphere each gamma-ray will have been transformed into about 200,000 visible photons. The neutrino, which only interacts through the Weak Force streams straight out of the sun.
- 2H + 1H --> 3He + gamma-ray
The Deuterium reacts with another proton to form 3He (2p+ & 1n) plus another gamma-ray. The first two reactions must happen twice to form two 3He nuclei.
- 3He + 3He --> 4He + 2 1H
The two 3He nuclei react to form 4He (2p+ & 2n) giving two protons "change" plus a bit of added kinetic of the product nuclei. Not that the 3He nuclei repel each other more strongly because they contain two positively charged protons. The initial reaction above can occur at temperatures as low as 1 million K, but the last reaction can only occur at temperatures greater than about 10 million K.
The individual nuclear reactions proceed rather slowly, and it is a very small fraction of nuclei in the core of the sun with enough energy to overcome the electrical repulsion. Even so, every second the sun turns 600 million tons of hydrogen into 596 million tons of helium (with 4 million tons transformed into luminous eneryy via E=mc2).
More massive stars burn hydrogen via a catalytic reaction called The CNO CYCLE. Because the initial step in the CNO Cycle requires a Carbon nucleus (6 p+) to react with a proton it requires higher temperatures and is much more temperature sensitive than the P-P Chain (The energy produced is proportional to T20 for the CNO cycle vs T4 for the P-P Chain). Stars of mass greater than about 1.2 M![]() with core temperatures, Tcore > 17 million K, produce most of their energy by the CNO cycle.
with core temperatures, Tcore > 17 million K, produce most of their energy by the CNO cycle.
The Triple-Alpha Process follows hydrogen burning in both solar-type stars and high-mass stars transforming Helium into Carbon. (n.b. Stars with M <>![]() will not reach high enough temperatures for the 3-alpha process.) There are no stable isotopes with Atomic Mass 5 or 8 (i.e. such that reactions like:
will not reach high enough temperatures for the 3-alpha process.) There are no stable isotopes with Atomic Mass 5 or 8 (i.e. such that reactions like:
- 4He + 1H --> 5X
- 4He + 4He --> 8X
may occur). The next stage in energy generation in stars is the Triple-Alpha Process which requires 3 - alpha particles (4He nuclei) to collide simultaneously to form Carbon:
- 4He + 4He + 4He --> 12C
This reaction requires both very high temperatures (T > 100 million K) and very high densities which will occur only after the star has exhausted its store of hydrogen and has a core of nearly pure helium. Only stars with masses greater than about 0.4M![]() will reach temperatures high enough to ignite the Triple-alpha process.
will reach temperatures high enough to ignite the Triple-alpha process.
Advanced Nuclear Burning Stages
Following the Triple-alpha process there are a variety of reactions which may occur depending on the mass of the star. Three general principles influence the roles that these nuclear burning stages may play:
- Successive nuclear burning stages, involving more massive nuclei with higher charges, will require increasingly high temperatures to overcome the increased electrical repulsion.
- The amount of energy released by each successive reaction stage decreases so that later nuclear burning stages become shorter and shorter.
- Once fusion reactions have produced an iron core, further fusion reactions no longer produce energy, but absorb energy from the stellar core. As we shall see this may have a catastrophic effect on the star as it nears the end of its life.
In stars like the sun, Carbon produced by helium burning via the Triple-alpha process will react with available helium nuclei to produce oxygen:
- 12C + 4He --> 160 + gamma-ray
with some production of Neon, but the extreme electrical repulsion makes it difficult to produce nuclei more massive than Neon via helium-capture.
- 160 + 4He --> 20Ne + gamma-ray
In more massive stars with temperatures greater than about 500 million K, Carbon burning will occur. This is just one of a variety of possible reactions:
- 12C + 12C --> 24Mg + gamma-ray
And above 1 billion K, Oxygen burning may occur; again with a variety of possible reaction products (e.g.Sulfur, as shown, Magnesium, Silicon & Phosphorus):
- 160 + 160 --> 32S + gamma-ray
Finally, at temperatures greater than about 3 billion K, Silicon burning occurs through a series of reactions that produce nuclei near the "iron-peak", that is near 56Fe on the Periodic Table, the element with the most strongly bound nucleus.
- Nuclear Reactions from the University of Oregon's Electronic Textbook.
Neutrinos were first "invented" by W. Pauli (of Exclusion Principle fame) in order to explain apparent failures in conservation of energy, momentum and leptons in certain nuclear decays. Pauli reasoned that these particles must be chargeless, have a mass much lower than the mass of the electron and interact only very weakly with other matter. He called them "neutrons", but when the massive baryon that we now call the neutron was discovered, it was realized that this could not be Pauli's particle and the name of the hypothetical particle was changed to "neutrino". The existence of the neutrino was confirmed by Reines and Cowan in 1956.
Although astrophysicists have great confidence in their calculations of the structure and evolution of stars like the sun, there is no substitute for experimental confirmation. Because the neutrinos are the only nuclear reaction products that make it out from the solar core, the most direct confirmation of the theories would be to measure the neutrinos emitted by the sun's P-P chain. The first experiment, begun in 1970 used a 100,000 gallon tank of cleaning fluid called perchloroethylene -- C2Cl4 to detect neutrinos from a subsidiary branch of the Proton-Proton Chain via the weak interaction:
37Cl + ![]() --> 37Ar + e-
--> 37Ar + e-
The experiment was placed a mile underground in the Homestake gold mine in Lead, SD to avoid contamination from other particle interactions. The experiment was predicted to create 3 Argon atoms, which could be counted by their radioactivity, every other day, but only about 1/3 that number were detected. The experiment has continued for over 20 years and has recently been joined by other solar neutrino experiments in Japan (Kamiokande), Russia (SAGE = Soviet(sic)-American Gallium Experiment) and Italy (GALLEX), all reporting the same result.
The most promising resolution of this problem lies in the physics of the neutrino itself. There are three flavors of leptons -- electrons (with their associated anti-particle the positron), muons and tau leptons, each with an associated flavor of neutrino, ![]() ,
, ![]() and
and ![]() . In an extension of the electroweak unified force theory it has been proposed that neutrinos can "oscillate" among these three flavors. If this theory is correct, then the electron neutrinos produced by the solar nuclear fusion reactions may be oscillating among flavors as they travel toward earth, producing the apparent deficit. One implication of this idea is that neutrinos must have a small but non-zero mass. Current limits place the mass of the electron neutrino at less than 1/100000 th the mass of the electron. Recent experimental results appear to confirm this theory.
. In an extension of the electroweak unified force theory it has been proposed that neutrinos can "oscillate" among these three flavors. If this theory is correct, then the electron neutrinos produced by the solar nuclear fusion reactions may be oscillating among flavors as they travel toward earth, producing the apparent deficit. One implication of this idea is that neutrinos must have a small but non-zero mass. Current limits place the mass of the electron neutrino at less than 1/100000 th the mass of the electron. Recent experimental results appear to confirm this theory.
Nuclear fission
n nuclear physics and nuclear chemistry, nuclear fission is a nuclear reaction in which the nucleus of an atom splits into smaller parts, often producing free neutrons and lighter nuclei, which may eventually produce photons (in the form of gamma rays). Fission of heavy elements is an exothermic reaction which can release large amounts of energy both as electromagnetic radiation and as kinetic energy of the fragments (heating the bulk material where fission takes place). Fission is a form of nuclear transmutation because the resulting fragments are not the same element as the original atom.
Nuclear fission produces energy for nuclear power and to drive the explosion of nuclear weapons. Both uses are made possible because certain substances called nuclear fuels undergo fission when struck by free neutrons and in turn generate neutrons when they break apart. This makes possible a self-sustaining chain reaction that releases energy at a controlled rate in a nuclear reactor or at a very rapid uncontrolled rate in a nuclear weapon.
The amount of free energy contained in nuclear fuel is millions of times the amount of free energy contained in a similar mass of chemical fuel such as gasoline, making nuclear fission a very tempting source of energy; however, the products of nuclear fission are radioactive and remain so for significant amounts of time, giving rise to a nuclear waste problem. Concerns over nuclear waste accumulation and over the destructive potential of nuclear weapons may counterbalance the desirable qualities of fission as an energy source, and give rise to ongoing political debate over nuclear power.
Nuclear fission differs from other forms of radioactive decay in that it can be harnessed and controlled via a chain reaction: free neutrons released by each fission event can trigger yet more events, which in turn release more neutrons and cause more fissions. Chemical isotopes that can sustain a fission chain reaction are called nuclear fuels, and are said to be fissile. The most common nuclear fuels are 235U (the isotope of uranium with an atomic mass of 235 and of use in nuclear reactors) and 239Pu (the isotope of plutonium with an atomic mass of 239). These fuels break apart into a bimodal range of chemical elements with atomic masses centering near 95 and 135 u (fission products). Most nuclear fuels undergo spontaneous fission only very slowly, decaying mainly via an alpha/beta decay chain over periods of millennia to eons. In a nuclear reactor or nuclear weapon, most fission events are induced by bombardment with another particle such as a neutron.
Typical fission events release about two hundred million eV of energy for each fission event. By contrast, most chemical oxidation reactions (such as burning coal or TNT) release at most a few eV per event, so nuclear fuel contains at least ten million times more usable energy than does chemical fuel. The energy of nuclear fission is released as kinetic energy of the fission products and fragments, and as electromagnetic radiation in the form of gamma rays; in a nuclear reactor, the energy is converted to heat as the particles and gamma rays collide with the atoms that make up the reactor and its working fluid, usually water or occasionally heavy water.
When uranium decays into two other atoms, there is produced an energy of ~200 MeV. Of this energy, 168 MeV is kinetic energy of uranium parts (atoms), which fly away with a speed of c/30. (See coulomb's power of protons.) Also there is emitted an average of 2.5 neutrons with kinetic energy of ~2 MeV each. Finally, the fission reaction emits ~30 MeV gamma photon.
Neutron and gamma rays emitted by fragments erase information about fission process itself, making difficult to study dynamics from saddle to scission point, where the fragments are formed and nuclear interaction dispels. Nevertheless there are few fission events for which no neutron nor gamma are emitted. These events are part of the so called cold fission[1].
In fission there is a preference to yield fragments with even proton numbers, which is called odd-even effect on fragments charge distribution. However, no odd-even effect is observed on fragment mass number distribution. This result is attributed to nucleon pair breaking in fission process.

Nuclear fission of heavy elements produces energy because the specific binding energy (binding energy per mass) of intermediate-mass nuclei with atomic numbers and atomic masses close to 61Ni and 56Fe is greater than the specific binding energy of very heavy nuclei, so that energy is released when heavy nuclei are broken apart.
The total rest masses of the fission products (Mp) from a single reaction is less than the mass of the original fuel nucleus (M). The excess mass Δm = M – Mp is the invariant mass of the energy that is released as photons (gamma rays) and kinetic energy of the fission fragments, according to the mass-energy equivalence formula E = mc².
In nuclear fission events the nuclei may break into any combination of lighter nuclei, but the most common event is not fission to equal mass nuclei of about mass 120; the most common event (depending on isotope and process) is a slightly unequal fission in which one daughter nucleus has a mass of about 90 to 100 u and the other the remaining 130 to 140 u.[2] Unequal fissions are energetically more favorable because this allows one product to be closer to the energetic minimum near mass 60 u (only a quarter of the average fissionable mass), while the other nucleus with mass 135 u is still not far out of the range of the most tightly bound nuclei (another statement of this, is that the atomic binding energy curve is slightly steeper to the left of mass 120 u than to the right of it).
The variation in specific binding energy with atomic number is due to the interplay of the two fundamental forces acting on the component nucleons (protons and neutrons) that make up the nucleus. Nuclei are bound by an attractive strong nuclear force between nucleons, which overcomes the electrostatic repulsion between protons. However, the strong nuclear force acts only over extremely short ranges, since it follows a Yukawa potential. For this reason large nuclei are less tightly bound per unit mass than small nuclei, and breaking a very large nucleus into two or more intermediate-sized nuclei releases energy.
Because of the short range of the strong binding force, large nuclei must contain proportionally more neutrons than do light elements, which are most stable with a 1–1 ratio of protons and neutrons. Extra neutrons stabilize heavy elements because they add to strong-force binding without adding to proton-proton repulsion. Fission products have, on average, about the same ratio of neutrons and protons as their parent nucleus, and are therefore usually unstable because they have proportionally too many neutrons compared to stable isotopes of similar mass. This is the fundamental cause of the problem of radioactive high level waste from nuclear reactors. Fission products tend to be beta emitters, emitting fast-moving electrons to conserve electric charge as excess neutrons convert to protons inside the nucleus of the fission product atoms.
The most common nuclear fuels, 235U and 239Pu, are not major radiologic hazards by themselves: 235U has a half-life of approximately 700 million years, and although 239Pu has a half-life of only about 24,000 years, it is a pure alpha particle emitter and hence not particularly dangerous unless ingested. Once a fuel element has been used, the remaining fuel material is intimately mixed with highly radioactive fission products that emit energetic beta particles and gamma rays. Some fission products have half-lives as short as seconds; others have half-lives of tens of thousands of years, requiring long-term storage in facilities such as Yucca Mountain until the fission products decay into non-radioactive stable isotopes.
Induced gamma emission
In physics, induced gamma emission (IGE) refers to the process of fluorescent emission of gamma rays from excited nuclei, usually involving a specific nuclear isomer. It is analogous to conventional fluorescence, which is defined to be the emission of a photon (light) by an excited electron in an atom or molecule. In the case of IGE, nuclear isomers can store significant amounts of excitation energy for times long enough for them to serve as "nuclear fluorescent" materials. There are over 800 known nuclear isomers[1] but almost all are too intrinsically radioactive to be considered for applications. As of 2006 there were 5 proposed[citation needed] nuclear isomers that appeared to be physically capable of IGE fluorescence in safe arrangements: tantalum-180m, osmium-187m, platinum-186m, hafnium-178m2 and zinc-66m.
Distinctive features
- If an incident photon is absorbed by an initial state of a target nucleus, that nucleus will be raised to a more energetic state of excitation. If that state can radiate its energy only during a transition back to the initial state, the result is a scattering process as seen in the schematic figure. That is not an example of IGE.
- If an incident photon is absorbed by an initial state of a target nucleus, that nucleus will be raised to a more energetic state of excitation. If there is a nonzero probability that sometimes that state will start a cascade of transitions as shown in the schematic, that state has been called a "gateway state" or "trigger level" or "intermediate state". One or more fluorescent photons are emitted, often with different delays after the initial absorption and the process is an example of IGE.
- If the initial state of the target nucleus is its ground (lowest energy) state, then the fluorescent photons will have less energy than that of the incident photon (as seen in the schematic figure). Since the scattering channel is usually the strongest, it can "blind" the instruments being used to detect the fluorescence and early experiments preferred to study IGE by pulsing the source of incident photons while detectors were gated off and then concentrating upon any delayed photons of fluorescence when the instruments could be safely turned back on.
- If the initial state of the target nucleus is a nuclear isomer (starting with more energy than the ground) it can also support IGE. However in that case the schematic diagram is not simply the example seen for 115In but read from right to left with the arrows turned the other way. Such a "reversal" would require simultaneous (to within <0.25>
- If the target is a nuclear isomer storing a considerable amount of energy then IGE might produce a cascade that contains a transition that emits a photon with more energy than that of the incident photon. This would be the nuclear analog of upconversion in laser physics.
- If the target is a nuclear isomer storing a considerable amount of energy then IGE might produce a cascade through a pair of excited states whose lifetimes are "inverted" so that in a collection of such nuclei, population would build up in the longer lived upper level while emptying rapidly from the shorter lived lower member of the pair. The resulting inversion of population might support some form of coherent emission analogous to amplified spontaneous emission (ASE) in laser physics. If the physical dimensions of the collection of target isomer nuclei were long and thin, then a sort of "gamma ray laser" might result.
- Since the IGE from ground state nuclei requires the absorption of very specific photon energies to produce delayed fluorescent photons that are easily counted, there is the possibility to construct energy-specific dosimeters by combining several different nuclides. This was demonstrated[7] for the calibration of the radiation spectrum from the DNA-PITHON pulsed nuclear simulator. Such a dosimeter could be useful in radiation therapy where X-ray beams may contain many energies. Since photons of different energies deposit their effects at different depths in the tissue being treated, it could help calibrate how much of the total dose would be deposited in the actual target volume.
- In theory, IGE materials based on nuclear isomers have a very high energy density compared to chemical sources. This makes them interesting as power sources if the cross section turns out to be useful in practice. For instance, a "nuclear battery" could be constructed by carefully adjusting the density of the IGE material to make it close to "critical", in which case a small application of the right energy gammas could cause the slow but continual release of more gammas due to stimulated emission. Converted to electricity, the gammas represent a powerful source of energy. Once the nuclei have all returned to the ground state, the "battery" could be re-charged by pumping it again.
- In February 2003, the non-peer reviewed New Scientist wrote about the possibility of an IGE-powered airplane.[8] The idea was to utilize 178m2Hf (presumably due to its high energy to weight ratio) which would be triggered to release gamma rays that would heat air in a chamber for jet propulsion. This power source is apparently called a "quantum nucleonic reactor", although it is not clear if this name exists only in reference to the New Scientist article.
- It is partly this theoretical density that has made the entire IGE field so controversial. It has been suggested that the materials might be constructed to allow all of the stored energy to be released very quickly in a "burst". The density of gammas produced in this reaction would be high enough that it might allow them to be used to compress the fusion fuel of a fusion bomb. If this turns out to be the case, it might allow a fusion bomb to be constructed with no fissile material inside (eg. a pure fusion weapon), and it is the control of the fissile material and the means for making it that underlies most attempts to stop nuclear proliferation. In fact, the possible energy release of the gammas alone would make IGE a potential high power "explosive" on its own, or a potential radiological weapon. Basic research remains in early stages but that has not deterred the worrying about these possibilities.
Societal concerns
Due to the possibility, no matter how remote, of IGE being used as a shortcut to, or analog of, a nuclear bomb, IGE has become a "hot topic" in the arms control field, where IGE is one of a number of theoretical "shortcuts" that are often discussed together. For instance, the apparently mythical red mercury is another proposed mechanism to build a "mini-nuke", and it is not uncommon to see references to red mercury as being either a ballotechnic or IGE material. As a result, it is not uncommon to see confusion about ballotechnic materials being the same thing as IGE's.
Spallation
In general, spallation is a process in which fragments of material (spall) are ejected from a body due to impact or stress. In nuclear physics, it is the process in which a heavy nucleus emits a large number of nucleons as a result of being hit by a high-energy particle, thus greatly reducing its atomic weight. In the context of impact physics it describes ejection or vaporization of material from a target during impact by a projectile. In planetary physics, spallation describes meteoritic impacts on a planetary surface and the effects of a stellar wind on a planetary atmosphere. In the context of mining or geology, spallation can refer to pieces of rock breaking off a rock face due to the internal stresses in the rock; it commonly occurs on mine shaft walls. In the context of anthropology, spallation is a process used to make stone tools such as arrowheads by knapping.
Nuclear spallation
Nuclear spallation occurs naturally in earth's atmosphere owing to the impacts of cosmic rays, and also on the surfaces of bodies in space such as meteorites and the moon. Evidence of cosmic ray spallation is evidence that the material in question has been exposed on the surface of the body of which it is part, and gives a means of measuring the length of time of exposure. The composition of the cosmic rays themselves also indicates that they have suffered spallation before reaching Earth, because the proportion of light elements such as Li, B,and Be in them exceeds average cosmic abundances; these elements in the cosmic rays were evidently formed from spallation of oxygen, nitrogen, carbon and perhaps silicon in the cosmic ray sources or during their lengthy travel here. Cosmogenic isotopes of aluminium, beryllium, chlorine, iodine and neon, formed by spallation of terrestrial elements under cosmic ray bombardment, have been detected on earth.
Nuclear spallation is one of the processes by which a particle accelerator may be used to produce a beam of neutrons. A mercury, tantalum or other heavy metal target is used, and 20 to 30 neutrons are expelled after each impact. Although this is a far more expensive way of producing neutron beams than by a chain reaction of nuclear fission in a nuclear reactor, it has the advantage that the beam can be pulsed with relative ease. The concept of nuclear spallation was first coined by Nobelist Glenn T. Seaborg in his doctoral thesis on the inelastic scattering of neutrons in 1937.[1]
Laser spallation
Laser induced spallation is a recent experimental technique developed to understand the adhesion of thin films with substrates. A high energy pulsed laser (typically Nd:YAG) is used to create a compressive stress pulse in the substrate wherein it propagates and reflects of as a tensile wave at the free boundary. This tensile pulse spalls/peels the thin film while propagating towards the substrate. Using theory of wave propagation in solids it is possible to extract the interface strength. The stress pulse created in this fashion is usually around 3-8 nanoseconds in duration while its magnitude varies as a function of laser fluence. Due to the non-contact application of load, this technique is very well suited to spall ultra-thin films (1 micrometre in thickness or less). It is also possible to mode convert a longitudinal stress wave into a shear stress using a pulse shaping prism and achieve shear spallation.
Production of neutrons at a spallation neutron source
Generally the production of neutrons at a spallation source begins with a high powered accelerator. This is more often than not a synchrotron. As an example, the ISIS neutron source is based on some components of the former Nimrod synchrotron. Nimrod was uncompetitive for high energy physics so it was replaced with a new synchrotron, initially using the original injectors, but which produces a highly intense pulsed beam of protons. Whereas Nimrod would produce around 2ųA at 7GeV, ISIS produces 200 ųA at 800 MeV. This is pulsed at the rate of 50 Hz, and this intense beam of protons is focused onto a target. Experiments have been done with depleted uranium targets but although these produce the most intense neutron beams, they also have the shortest lives. Generally, therefore, tantalum targets have been used. Spallation processes in the target produce the neutrons, initially at very high energies - a good fraction of the proton energy. These neutrons are then slowed in moderators filled with liquid hydrogen or liquid methane to the energies that are needed for the scattering instruments. Whilst protons can be focused since they have charge, chargeless neutrons cannot be, so in this arrangement the instruments are arranged around the moderators.
Inertial fusion energy has the potential to produce orders of magnitude more neutrons than spallation. Neutrons are capable of locating hydrogen atoms in structures, resolving atomic thermal motion and studying collective excitations of photons more effectively than X-rays.


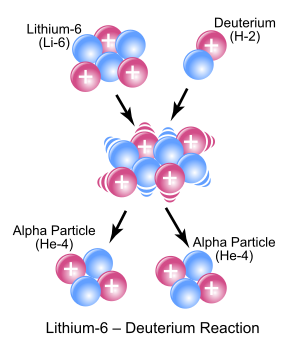
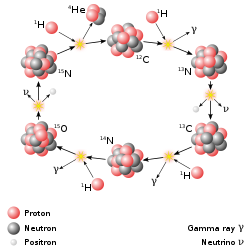

No comments:
Post a Comment